Дефазировка

Потери когерентности в полости из-за дефазировки.

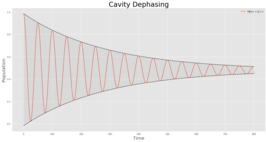
В физике дефазировка — это механизм, восстанавливающий классическое поведение квантовой системы. Она относится к способам, которыми когерентность вызванная возмущением со временем затухает, и система возвращается в состояние до возмущения. Это важный эффект в молекулярной и атомной спектроскопии, а также в физике конденсированного состояния мезоскопических устройств.

Мезоскопика

Причину можно понять, описав проводимость в металлах как классическое явление с квантовыми эффектами, которые все встроены в подвижность, которую можно вычислить квантово-механически, как также происходит с сопротивлением, которое можно рассматривать как эффект рассеяния электронов проводимости. Когда температура понижается и размеры устройства значительно уменьшаются, это классическое поведение должно исчезнуть, и законы квантовой механики должны управлять поведением проводящих электронов, рассматриваемых как волны, которые движутся баллистически внутри проводника без какой-либо диссипации. Чаще всего именно это и наблюдают. тем не менее обнаружилось, что так называемое время дефазировки, то есть время, которое требуется проводящим электронам, чтобы потерять свое квантовое поведение, становится конечным, а не бесконечным, когда температура приближается к нулю в мезоскопических устройствах, что противоречит ожиданиям теории Бориса Альтшулера, Аркадий Аронов и Давид Э. Хмельницкий. Такое насыщение времени дефазировки при низких температурах является открытой проблемой, даже несмотря на то, что было выдвинуто несколько предложений.

Спектроскопия

Когерентность образца объясняется недиагональными элементами матрицы плотности. Внешнее электрическое или магнитное поле может создать когерентность между двумя квантовыми состояниями в образце, если частота соответствует энергетической щели между двумя состояниями. Влияние когерентности затухает со временем из-за сбоя фазы или спин-спиновой релаксации, T₂.

После создания когерентности в образце светом образец излучает волну поляризации, частота которой равна частоте падающего света, а фаза инвертируется относительно фазы падающего света. Кроме того, образец возбуждается падающим светом и генерируется молекулы в возбужденном состоянии. Свет, проходящий через образец, поглощается из-за этих двух процессов, и это выражается в спектре поглощения. Когерентность спадает с постоянной времени T₂, и интенсивность волны поляризации уменьшается. Население возбужденного состояния также убывает с постоянной времени продольной релаксации T₁. Постоянная времени T₂ обычно намного меньше, чем T₁, и ширина полосы спектра поглощения связана с этими постоянными времени через преобразование Фурье, поэтому постоянная времени T₂ является основным фактором, влияющим на ширину полосы. Постоянная времени T₂ была измерена непосредственно с помощью сверхбыстрой спектроскопии с временным разрешением, например, в экспериментах с фотонным эхом.

Рекомендации

Литература

• Imry, Y. Introduction to Mesoscopic Physics. (And references therein.)
• Aleiner, I. L. (1999). "Comment on "Quantum Decoherence in Disordered Mesoscopic Systems"". Physical Review Letters. 82 (15): 3190. arXiv:cond-mat/9808078. Bibcode:1999PhRvL..82.3190A. doi:10.1103/PhysRevLett.82.3190.
• Cohen, D. (1999). "Dephasing at low temperatures". Physical Review B. 59 (17): 11143—11146. arXiv:cond-mat/9807038. Bibcode:1999PhRvB..5911143C. doi:10.1103/PhysRevB.59.11143.
• Golubev, D. S. (2003). "Low-temperature dephasing and Renormalization in model systems". Journal of the Physical Society of Japan. 72 (Suppl. A): 30—35. arXiv:cond-mat/0208548. Bibcode:2003JPSJ...72S..30S. doi:10.1143/JPSJS.72SA.30.
• Saminadayar, L. (2007). "Electron coherence at low temperatures: The role of magnetic impurities". Physica E. 40 (1): 12—24. arXiv:0709.4663. Bibcode:2007PhyE...40...12S. doi:10.1016/j.physe.2007.05.026.
• Mohanty, P. Complexity from Microscopic to Macroscopic Scales: Coherence and Large deviations.
• Frasca, M. (2003). "Saturation of dephasing time in mesoscopic devices produced by a ferromagnetic state". Physical Review B. 68 (19): 193413. arXiv:cond-mat/0308377. Bibcode:2003PhRvB..68s3413F. doi:10.1103/PhysRevB.68.193413.