Распределение Максвелла

Функция плотности распределения для 10⁶ молекул кислорода при −100, 20, 600 градусах Цельсия

Распределе́ние Ма́ксвелла — общее наименование нескольких распределений вероятности, которые описывают статистическое поведение параметров частиц идеального газа. Вид соответствующей функции плотности вероятности диктуется тем, какая величина: скорость частицы, проекция скорости, модуль скорости, энергия, импульс и т. д. — выступает в качестве непрерывной случайной величины. В ряде случаев распределение Максвелла может быть выражено как дискретное распределение по множеству уровней энергии.

Наиболее значимое распределение Максвелла записывается для модуля скорости частицы $v$ в непрерывном случае и имеет плотность:

$f_{v}(x)=Bx^{2}\exp \left[-\beta x^{2}\right]\,\,(x\geq 0)$ и $f_{v}(x)=0\,\,(x<0),$

где $x$ — формальная переменная, фактор $\beta >0$ определяется типом частиц и температурой, а множитель $B$ подбирается в зависимости от $\beta$ для обеспечения нормировки. Именно это выражение считается максвелловским распределением в математике, хотя для других параметров частиц аналитический вид распределения Максвелла будет иным.

Распределение Максвелла лежит в основе кинетической теории газов, объясняющей многие фундаментальные свойства газов, включая давление и диффузию. С его помощью вычисляются средние и наиболее вероятные скорости и энергии молекул газа. Оно также применимо для описания электронных процессов переноса и других явлений в физике и химии. Распределение Максвелла может быть получено при помощи статистической механики (см. происхождение статсуммы). Данное распределение является реализующимся с наивысшей вероятностью распределением изучаемого параметра.

Сфера применения распределения Максвелла

Требования к описываемой системе, примеры

Вопрос о применимости распределения Максвелла к конкретной системе равносилен вопросу о том, может ли эта система считаться идеальным газом с достаточной точностью. При этом система должна

• состоять из большого числа частиц и находиться в термодинамическом равновесии;
• являться изотропной;
• являться классической, то есть релятивистские и квантовые эффекты должны быть малы;
• быть столкновительно-доминируемой (взаимодействие частиц допускается лишь в случае, когда оно зависит только от относительного положения частиц, в частности, допускаются абсолютно упругие соударения).

Такой набор требований удовлетворяется в первую очередь в газах, например в воздухе, при обычных условиях. Распределение Максвелла применимо к множеству свойств индивидуальных молекул в газе. В первую очередь о нём обычно думают, как о распределении энергий молекул в газе, но оно может применяться к распределению скоростей и других параметров молекул. Чаще всего оно является непрерывным распределением по континууму изменения случайного параметра.

Во многих случаях, однако, условие доминирования упругих соударений над всеми другими процессами не выполняется даже приблизительно. Так, в физике ионосферы и космической плазмы, большое значение имеют процессы рекомбинации и столкновительного возбуждения (то есть излучательные процессы), в особенности для электронов. Использование распределения Максвелла в этом случае не только дало бы количественно неверные результаты, но и привело бы к качественно неправильной интерпретации соответствующих процессов.

Условия классического рассмотрения

В случаях, где квантовая дебройлева длина волны частиц газа не является малой по сравнению с расстоянием между частицами, наблюдаются отклонения от распределения Максвелла из-за квантовых эффектов. Поэтому важен вопрос о границах применимости классического рассмотрения.

Соотношение неопределённостей (нередко упрощённо записываемое в форме $\Delta x\cdot \Delta p_{x}\sim h,$ где $\Delta x,$ $\Delta p_{x}$ — неопределённости координаты и $x$-проекции импульса, $h$ — постоянная Планка) имеет трёхмерный аналог вида $r\cdot p\sim h,$ где $r$ обозначает характерный линейный размер зоны локализации частицы. Чтобы неопределённости в координате и импульсе не играли роли и могла применяться классическая, а не квантовая механика, должно выполняться соотношение:

$V^{1/3}\cdot p\gg h,$

где $V$ — объём, на который в среднем приходится одна частица, равный обратной концентрации $n^{-1}$ частиц газа. Если возвести обе части в квадрат, получится:

$n^{-{\frac {2}{3}}}h^{-2}p^{2}\gg 1.$

Учитывая, что $p^{2}=2mE$ и беря в качестве характерного значения энергии величину $(3/2)kT,$ придём к:

$T\gg {\frac {n^{\frac {2}{3}}h^{2}}{3mk}}=T_{deg}\qquad$ ($T_{deg}$ — температура вырождения, а $m$ — масса частицы).

При температурах ниже $T_{deg}$ распределение Максвелла неприменимо.

Распределение Максвелла по состояниям

Распределение Максвелла можно записать как дискретное распределение по множеству состояний молекулы, нумеруемых символом $i$:

${\frac {N_{i}}{N}}={\frac {\exp \left(-E_{i}/kT\right)}{\sum _{j}^{}{\exp \left(-E_{j}/kT\right)}}}$.

Через $E_{i}$ и $N_{i}$ обозначены энергия молекулы в $i$-м состоянии и число таких молекул соответственно, $T$ — температура системы, $N$ — общее число молекул в системе и $k$ — постоянная Больцмана. (Бывает, что вышеупомянутое уравнение записывается с множителем $g_{i}$, обозначающим степень вырождения энергетических уровней. В этом случае $i$ нумерует не состояния, а энергии и сумма будет по энергиям, а не по состояниям). Поскольку скорость связана с энергией, последнее уравнение может использоваться для получения связи между температурой и скоростями молекул в газе. Знаменатель известен как каноническая статистическая сумма.

Разновидности непрерывного распределения Максвелла

Представленный в этом разделе вывод распределений Максвелла, естественный для современной учебно-методической литературы, отличается от вывода, предложенного самим Джеймсом Клерком Максвеллом и позже описанного с меньшим количеством предположений Людвигом Больцманом. Исторический вывод будет приведён в конце статьи.

Распределение по вектору импульса

В случае идеального газа из невзаимодействующих молекул вся энергия находится в форме кинетической энергии. Кинетическая энергия соотносится с импульсом частицы как:

$E={\frac {p^{2}}{2m}}$,

где $p^{2}$ — квадрат вектора импульса $\mathbf {p} =[p_{x},p_{y},p_{z}]$, тогда

${\frac {N_{i}}{N}}={\frac {1}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]$,

где $Z$ — статсумма, соответствующая знаменателю выражения для $N_{i}/N$ из предыдущего раздела, $m$ — масса молекулы.

Если уровни энергии расположены достаточно густо, факт дискретности становится непринципиальным и можно считать, что энергии распределены непрерывно. Тогда отношение $N_{i}/N$ пропорционально функции плотности вероятности $f_{\mathbf {p} }$ нахождения молекулы в состоянии с этими значениями компонент импульса. Таким образом:

$f_{\mathbf {p} }(p_{x},p_{y},p_{z})={\frac {C}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]$.

Постоянная $C$ определяется из условия нормировки, в соответствии с которым вероятность того, что молекулы имеют какой-либо вообще импульс, должна быть равна единице. Поэтому интеграл $f_{\mathbf {p} }$ по всем значениям $p_{x}\,,p_{y}$ и $p_{z}$ должен быть равен единице. Можно показать, что

$\iiint \limits _{-\infty }^{+\infty }{\frac {1}{Z}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]\,dp_{x}\,dp_{y}\,dp_{z}={\frac {1}{Z}}\left(2\pi mkT\right)^{3/2}$.

Таким образом, чтобы интеграл имел значение 1 необходимо, чтобы

$C={\frac {Z}{({\sqrt {2\pi mkT}})^{3}}}$.

Подставляя такое $C$ в уравнение для $f_{\mathbf {p} }$ и используя тот факт, что $p_{i}=mv_{i}$, мы получим:

$f_{\mathbf {p} }(p_{x},p_{y},p_{z})={\sqrt {\left({\frac {1}{2\pi mkT}}\right)^{3}}}\exp \left[{\frac {-(p_{x}^{2}+p_{y}^{2}+p_{z}^{2})}{2mkT}}\right]$.

Распределение по вектору скорости

Учитывая, что плотность распределения по скоростям $f_{\mathbf {v} }$ пропорциональна плотности распределения по импульсам:

$f_{\mathbf {v} }d^{3}v=f_{\mathbf {p} }\left({\frac {dp}{dv}}\right)^{3}d^{3}v$,

и используя $\mathbf {p} =m\mathbf {v}$, получим:

$f_{\mathbf {v} }(v_{x},v_{y},v_{z})={\sqrt {\left({\frac {m}{2\pi kT}}\right)^{3}}}\exp \left[{\frac {-m(v_{x}^{2}+v_{y}^{2}+v_{z}^{2})}{2kT}}\right]$,

что является распределением Максвелла по трём декартовым проекциям скоростей. Вероятность обнаружения частицы в бесконечно малом элементе $dv_{x}\,,dv_{y}\,,dv_{z}$ около скорости $\mathbf {v} =[v_{x},v_{y},v_{z}]$ равна:

$f_{\mathbf {v} }\left(v_{x},v_{y},v_{z}\right)dv_{x}dv_{y}dv_{z}$.

Распределение по проекции скорости

Распределение Максвелла для вектора скорости $[v_{x},v_{y},v_{z}]$ — является произведением распределений для каждого из трёх направлений:

$f_{v}\left(v_{x},v_{y},v_{z}\right)=f_{v}(v_{x})f_{v}(v_{y})f_{v}(v_{z}),$

где распределение по одному направлению:

$f_{v}(v_{i})={\sqrt {\frac {m}{2\pi kT}}}\exp \left[{\frac {-mv_{i}^{2}}{2kT}}\right]$.

Это распределение имеет форму нормального распределения. Как и следует ожидать для покоящегося газа, средняя скорость в любом направлении равна нулю.

Распределение по модулю импульса

Интегрируя, мы можем найти распределение по абсолютной величине импульса:

$f_{p}=\int _{\theta =0}^{\pi }\int _{\phi =0}^{2\pi }~f_{\mathbf {p} }p^{2}\sin(\theta )\,d\theta \,d\phi =4\pi {\sqrt {\left({\frac {1}{2\pi mkT}}\right)^{3}}}~p^{2}\exp \left[{\frac {-p^{2}}{2mkT}}\right].$

Распределение по энергии

Наконец, используя соотношения $p^{2}=2\,mE$ и $f_{E}\,dE=f_{p}\,dp$, мы получаем распределение по кинетической энергии:

$f_{E}=f_{p}{\frac {dp}{dE}}={\frac {2\pi }{\sqrt {(\pi kT)^{3}}}}{\sqrt {E}}{}~\exp \left[{\frac {-E}{kT}}\right].$

Распределение по модулю скорости

Часто более интересно распределение по абсолютному значению, а не по проекциям скоростей молекул. Модуль скорости, $v$ определяется как

$v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}$,

он всегда неотрицателен. Так как все $v_{i}$ распределены нормально, $v^{2}$ будет иметь хи-квадрат распределение с тремя степенями свободы. Если $f(v)$ — функция плотности вероятности для модуля скорости, то

$f\left(v\right)dv=P(\chi ^{2}|3)d\chi ^{2}$,

где $\chi ^{2}=mv^{2}/kT$. Таким образом, функция плотности вероятности для модуля скорости равна

$f(v)dv=4\pi v^{2}\left({\frac {m}{2\pi kT}}\right)^{3/2}\exp \left({\frac {-mv^{2}}{2kT}}\right)dv$.

Вид функции $f(v)$ соответствует приведённому в преамбуле с тем отличием, что там используется формальная переменная $x$ ради большей математической общности.

Характерные скорости молекул идеального газа

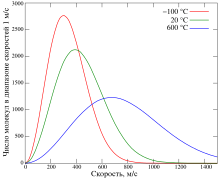
Уравнение для $f(v)dv$ даёт распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость. Но часто более интересны другие величины. Ниже будут определены наиболее вероятная, средняя и среднеквадратичная скорости.

Наиболее вероятная скорость

Наиболее вероятная скорость, $v_{p}$, — скорость, вероятность обладания которой любой молекулой системы максимальна и которая соответствует максимальному значению плотности вероятности распределения $f(v)$ (а значит, соответствует моде этого распределения). Чтобы найти её, необходимо вычислить $df/dv$, приравнять нулю и решить относительно $v$:

${\frac {df(v)}{dv}}=\left({\frac {m}{2\pi kT}}\right)^{3/2}\exp \left(-mv^{2}/2kT\right)\left[8\pi v+4\pi v^{2}(-mv/kT)\right]=0$,

$v_{p}={\sqrt {\frac {2kT}{m}}}={\sqrt {\frac {2RT}{\mu }}}$,

где $m$ — масса рассматриваемой частицы, $\mu$ — молярная масса.

Средняя скорость

$\langle v\rangle =\int \limits _{0}^{\infty }v\,f(v)\,dv$.

Подставляя $f(v)$ и интегрируя, мы получим

$\langle v\rangle ={\sqrt {\frac {8kT}{\pi m}}}={\sqrt {\frac {8RT}{\pi \mu }}}$.

Среднеквадратичная скорость

$\langle v'^{2}\rangle =\int \limits _{0}^{\infty }v^{2}\,f(v)\,dv$.

Подставляя $f(v)$ и интегрируя, мы получим:

${\sqrt {\langle v'^{2}\rangle }}={\sqrt {\frac {3kT}{m}}}={\sqrt {\frac {3RT}{\mu }}}$.

Исторический вывод распределения Максвелла

Получим теперь формулу распределения так, как это делал сам Максвелл.

Рассмотрим пространство скоростных точек (каждую скорость молекулы представляем как точку (скоростную точку) в системе координат $Ov_{x}v_{y}v_{z}$ в стационарном состоянии газа. Выберем бесконечно малый элемент объёма $dv_{x}dv_{y}dv_{z}$. Так как газ стационарный, количество скоростных точек в $dv_{x}dv_{y}dv_{z}$ остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функции плотности вероятности для всех направлений одинаковы.

$dP(v_{x})=\varphi (v_{x})dv_{x}\qquad dP(v_{y})=\varphi (v_{y})dv_{y}\qquad dP(v_{z})=\varphi (v_{z})dv_{z}$

Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента $v_{x}$ скорости молекулы не зависит от $y$- и $z$- компонент.

$dP(v_{x},v_{y},v_{z})=\underbrace {\varphi (v_{x})\varphi (v_{y})\varphi (v_{z})} _{f(v)}dv_{x}dv_{y}dv_{z}$ — фактически вероятность нахождения скоростной точки в объёме $dv_{x}dv_{y}dv_{z}$.

$f(v)=\varphi (v_{x})\varphi (v_{y})\varphi (v_{z})$

$\ln f(v)=\ln \varphi (v_{x})+\ln \varphi (v_{y})+\ln \varphi (v_{z})\quad {\bigg |}\quad {\frac {\partial }{\partial v_{x}}}$

${\frac {f'(v)}{f(v)}}{\frac {\partial v}{\partial v_{x}}}={\frac {\varphi '(v_{x})}{\varphi (v_{x})}}$

${\frac {\partial v}{\partial v_{x}}}={\frac {v_{x}}{v}}$

${\frac {1}{v}}{\frac {f'(v)}{f(v)}}={\frac {1}{v_{x}}}{\frac {\varphi '(v_{x})}{\varphi (v_{x})}}$

Правая часть не зависит от $v_{y}$ и $v_{z}$, значит и левая от $v_{y}$ и $v_{z}$ не зависит. Однако $v_{x}$ и $v_{y}$ равноправны, следовательно левая часть не зависит также и от $v_{x}$. Значит данное выражение может лишь равняться некоторой константе.

${\frac {1}{v}}{\frac {f'(v)}{f(v)}}=-\alpha$

${\frac {\varphi '(v_{x})}{\varphi (v_{x})}}=-\alpha v_{x}$

$\varphi (v_{x})=Ae^{-{\frac {\alpha {v_{x}}^{2}}{2}}}$

$\int \limits _{-\infty }^{\infty }\varphi (v_{x})\,dv_{x}=1\qquad \Rightarrow \qquad A\int \limits _{-\infty }^{\infty }e^{-{\frac {\alpha {v_{x}}^{2}}{2}}}\,dv_{x}=A\,{\sqrt {\frac {2}{\alpha }}}\,{\sqrt {\pi }}=1\qquad \Rightarrow \qquad A={\sqrt {\frac {\alpha }{2\pi }}}$

$\varphi (v_{x})={\sqrt {\frac {\alpha }{2\pi }}}e^{-{\frac {\alpha {v_{x}}^{2}}{2}}}$

Теперь нужно сделать принципиальный шаг — ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):

$\left\langle {\frac {mv^{2}}{2}}\right\rangle ={\frac {3}{2}}kT,$

где $k=1{,}380649\cdot 10^{-23}$ Дж/К — постоянная Больцмана.

$v={\sqrt {v_{x}^{2}+v_{y}^{2}+v_{z}^{2}}}.$

Ввиду равноправия всех направлений:

$\langle v_{x}^{2}\rangle =\langle v_{y}^{2}\rangle =\langle v_{z}^{2}\rangle ={\frac {1}{3}}\langle v^{2}\rangle ={\frac {kT}{m}}.$

Чтобы найти среднее значение $v_{x}^{2}$, проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:

${\frac {kT}{m}}=\int \limits _{-\infty }^{\infty }{v_{x}}^{2}\,\varphi (v_{x})\,dv_{x}={\sqrt {\frac {\alpha }{2\pi }}}\,\int \limits _{-\infty }^{\infty }v_{x}^{2}\,e^{-{\frac {\alpha {v_{x}}^{2}}{2}}}\,dv_{x}=$

$\qquad ={\sqrt {\frac {\alpha }{2\pi }}}\left[-2\,{\frac {d}{d\alpha }}\,\int \limits _{-\infty }^{\infty }e^{-{\frac {\alpha {v_{x}}^{2}}{2}}}\,dv_{x}\right]=-2\,{\sqrt {\frac {\alpha }{2\pi }}}\,{\frac {\delta }{\delta \alpha }}{\sqrt {\frac {2\pi }{\alpha }}}=-2{\sqrt {\alpha }}(-{\frac {1}{2}}\alpha ^{-{\frac {3}{2}}})={\frac {1}{\alpha }}.$

Отсюда найдём $\alpha$:

$\alpha ={\frac {m}{kT}}.$

Функция распределения плотности вероятности для $v_{x}$ (для $v_{y}$ и $v_{z}$ аналогично):

$\varphi (v_{x})=\left({\frac {m}{2\pi kT}}\right)^{\frac {1}{2}}\,e^{-{\frac {mv_{x}^{2}}{2kT}}}.$

Теперь рассмотрим распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости $v\subset [v;v+dv]$ лежат в шаровом слое радиуса $v$ и толщины $dv$, и $dv_{x}dv_{y}dv_{z}$ — объём элемента этого шарового слоя.

$dP(v_{x},v_{y},v_{z})=\varphi (v_{x})\varphi (v_{y})\varphi (v_{z})dv_{x}dv_{y}dv_{z}$

$\underbrace {dP(v_{x},v_{y},v_{z})} _{dP(v)}=\left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}\,e^{-{\frac {mv_{x}^{2}+mv_{y}^{2}+mv_{z}^{2}}{2kT}}}\underbrace {dv_{x}dv_{y}dv_{z}} _{4\pi v^{2}dv}$

$dP(v)=\underbrace {4\pi \,\left({\frac {m}{2\pi kT}}\right)^{\frac {3}{2}}\,v^{2}\,e^{-{\frac {mv^{2}}{2kT}}}} _{F(v)}dv$

Таким образом, мы получили функцию плотности вероятности $F(v)$, являющуюся распределением Максвелла.

См. также

• Статистика Бозе — Эйнштейна
• Статистика Ферми — Дирака
• Статистика Максвелла — Больцмана
• Опыт Ламмерта
• Опыт Штерна
• Распределение Гиббса
• Распределение Бозе — Эйнштейна
• Распределение Ферми — Дирака

Ссылки

http://www.falstad.com/gas/