Теорема Брахмагупты

${\overline {BD}}\perp {\overline {AC}},{\overline {EF}}\perp {\overline {BC}}$ $\Rightarrow |{\overline {AF}}|=|{\overline {FD}}|$

Теоре́ма Брахмагу́пты — теорема элементарной геометрии, найденная в седьмом столетии нашей эры индийским математиком Брахмагуптой.

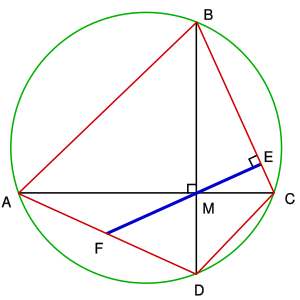
Если вписанный четырёхугольник имеет перпендикулярные диагонали, пересекающиеся в точке $M$, то прямая, проходящая через точку $M$ и перпендикулярная одной из его сторон, делит противоположную ей сторону пополам.

Замечание. По аналогии с серединным перпендикуляром (медиатрисой) к стороне треугольника отрезок $FE$ (на рисунке справа) называют антимедиатрисой противоположных сторон четырёхугольника. С учётом этого замечания теорема Брахмагупты может быть сформулирована в виде:

Две пары антимедиатрис вписанного ортодиагонального четырёхугольника проходят через точку пересечения его диагоналей.

Доказательство

На рисунке изображён вписанный четырёхугольник $ABCD$, имеющий перпендикулярные диагонали $AC$ и $BD$, а прямая $ME$ перпендикулярна стороне $BC$ и пересекает сторону $DA$ в точке $F$. Тогда $\angle {DMF}=\angle {BME}=\angle {MCE}\equiv \angle {ACB}=\angle {ADB}\equiv \angle {FDM}.$ Следовательно, треугольник $FMD$ — равнобедренный. Аналогично, равнобедренным будет и треугольник $FAM$. Поэтому $|FA|=|FM|=|FD|$.

Антицентр и коллинеарность

Четыре отрезка прямых, перпендикулярных одной стороне вписанного ортодиагонального четырёхугольника и проходящих через середину противоположной стороны, пересекаются в одной точке. Эта точка пересечения называется антицентром. Антицентр симметричен центру описанной окружности относительно «вершинного центроида». Таким образом, во вписанном четырёхугольнике центр описанной окружности, «вершинный центроид» и антицентр лежат на одной прямой.

Обобщения

• Известна теорема: Если в четырёхугольнике перпендикулярны диагонали, то на одной окружности (окружность восьми точек четырёхугольника) лежат восемь точек: середины сторон и проекции середин сторон на противоположные стороны . Из этой теоремы и теоремы Брахмагупты следует, что концы двух пар антимедиатрис (восемь точек) вписанного ортодиагонального четырёхугольника лежат на одной окружности (окружность восьми точек четырёхугольника).

Эта теорема обобщает теорему Брахмагупты, однако отсутствие вписанности четырёхугольника в окружность приводит к тому, что его антимедиатрисы пересекаются не в точке, являющейся точкой пересечения его диагоналей.

Литература

• Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. — М.: Наука, 1978. — Т. 14. — (Библиотека математического кружка).
• Понарин Я. П. Элементарная геометрия. В 2 т. — М.: МЦНМО, 2004. — ISBN 5-94057-170-0.
• Nathan Altshiller-Court. College geometry : an introduction to the modern geometry of the triangle and the circle. — Dover Publications, Inc., 2007. — ISBN 0-486-45805-9.
• Ross Honsberger. Episodes in Nineteenth and Twentieth Century Euclidean Geometry. — Mathematical Association of America, 1995. — Vol. 37. — P. 17—26. — (New Mathematical Library). — ISBN 0-88385-639-5 (Vol. 37). — ISBN 0-88385-600-X (complete set).
• Математика в задачах. Сборник материалов выездных школ команды Москвы на Всероссийскую математическую олимпиаду / Под редакцией А. А. Заславского, Д. А. Пермякова, А. Б. Скопенкова, М. Б. Скопенкова и А. В. Шаповалова.. — Москва: МЦНМО, 2009. — ISBN 978-5-94057-477-4.