Вращение Солнца

Вращение Солнца вокруг своей оси, заснятое с 30 марта по 29 апреля 2011 года.

Параметры вращения Солнца (англ. Solar rotation) зависят от широты места. Солнце не является твёрдым телом, оно состоит из газообразной плазмы. Точки на разных широтах вращаются с разными периодами, то есть вращение Солнца является дифференциальным. Причина дифференциальности вращения в настоящее время является одним из вопросов солнечной астрономии. Скорость вращения является наибольшей на экваторе Солнца (широта $\varphi$ = 0°) и уменьшается при движении к полюсам. Период вращения Солнца равен 25,34 земным суткам на экваторе и почти 38 суткам вблизи полюсов.

Уравнение вращения

Скорость при дифференциальном вращении можно описать уравнением

$\omega =A+B\,\sin ^{2}(\varphi )+C\,\sin ^{4}(\varphi ),$

где ω является угловой скоростью, выражаемой в градусах в сутки, φ — широта, A, B и C — постоянные. Значения A, B и C различаются в зависимости от того, каким методом проводились измерения, а также от величины периода наблюдений. В настоящее время используются такие средние значения:

$A=14.713\pm 0.0491^{\circ }/$сут,

$B=-2.396\pm 0.188^{\circ }/$сут,

$C=-1.787\pm 0.253^{\circ }/$сут.

Сидерическое вращение

На экваторе период вращения Солнца равен 24,47 суток. Эта величина называется сидерическим периодом вращения, её не следует путать с синодическим периодом вращения, равным 26,24 суткам и представляющим промежуток времени, спустя который для наблюдателя на Земле деталь поверхности Солнца повторит своё положение. Синодический период превышает сидерический, поскольку при повторении положения детали на поверхности Солнце совершает не только один оборот, но и поворот на небольшой дополнительный угол, компенсирующий смещение Земли по своей орбите. Заметим, что в астрофизической литературе обычно не используют период вращения на экваторе, вместо этого определяют кэррингтоновское вращение: синодический период обращения равен 27,2753 суткам, сидерический период составляет 25,38 суток. Такие значения периода соответствуют прямому вращения на широте 26° к северу или к югу от экватора, что является характерным значением для области возникновения солнечных пятен и проявлений периодической солнечной активности. При наблюдении с северного полюса эклиптики Солнце вращается против часовой стрелки. Если человек находится на северном полюсе Земли, то ему будет казаться, что солнечные пятна движутся слева направо по диску Солнца.

Число Бартельса

Вращательное число Бартельса является порядковым номером, характеризующим число оборотов Солнца при наблюдении с Земли. Используется для слежения за повторяющимися или смещающимися проявлениями солнечной активности. Предполагается, что каждый оборот длится 27 дней, что близко к синодическому периоду по Кэррингтону. Юлиус Бартельс в качестве начала отсчёта числа оборотов принял дату 8 февраля 1832 года. Порядковое число оборотов может являться своего рода календарём, согласующимся с периодами повторения солнечных и геофизических параметров.

Кэррингтоновское вращение

Видео, показывающее пять лет солнечного вращения. Каждый кадр соответствует одному кэррингтоновскому периоду.

Кэррингтоновское вращение представляет собой систему для сопоставления положений деталей на поверхности Солнца, разделённых некоторым промежутком времени, что позволяет отслеживать эволюцию групп солнечных пятен или вспышек.

Поскольку параметры вращения Солнца меняются с широтой, глубиной слоя и со временем, то подобные системы сравнения носят приблизительный характер. В случае модели кэррингтоновского вращения период обращения Солнца принят равным 27,2753 суткам. Каждый оборот Солнца в такой схеме обладает собственным номером, началом отсчёта которого является 9 ноября 1853 года. (Число Бартельса строится по подобной схеме, но период обращения принимается равным 27 суткам, началом отсчёта является 8 февраля 1832 года.)

Гелиографическая долгота детали на поверхности Солнца соответствует угловому расстоянию от объекта до центрального меридиана, то есть до линии от Солнца до Земли. Кэррингтоновская долгота детали является угловым расстоянием относительно фиксированной точки, положение которой указал Кэррингтон.

Ричард Кэррингтон определил скорость вращения Солнца по данным о солнечных пятнах на низких широтах в 1850-х гг., по его оценкам сидерический период обращения Солнца равен 25,38 суток. Сидерическое вращение измеряется относительно далёких звёзд, но, поскольку Земля вращается вокруг Солнца, то для земного наблюдателя период вращения Солнца будет равен 27,2753 суток.

Можно построить диаграмму, в которой долгота пятен откладывается по горизонтальной оси, а время — по вертикальной. Долгота измеряется по времени пересечения центрального меридиана и основывается на кэррингтоновской модели вращения. Если нарисовать на такой диаграмме положение солнечных пятен после каждого оборота, то большая часть новых точек окажется строго ниже точек от предыдущих оборотов. На протяжении длительных временных интервалов возможны небольшие смещения вправо или влево.

Использование солнечных пятен для измерения вращения

Постоянные в модели вращения были определены при измерении движения различных деталей поверхности Солнца. Наиболее известными такими деталями являются солнечные пятна. Хотя пятна наблюдались с древних времён, но только при изобретении телескопа выяснилось, что они вращаются вместе с Солнцем, поэтому можно определить период вращения Солнца. Английский исследователь Томас Хэрриот, вероятно, является первым, кто наблюдал солнечные пятна в телескоп, что доказывается зарисовками в тетради, датированными 8 декабря 1610 года. Результаты наблюдений Иоганна Фабрициуса, систематически наблюдавшего пятна в течение нескольких месяцев, были опубликованы в июне 1611 года под заголовком “De Maculis in Sole Observatis, et Apparente earum cum Sole Conversione Narratio” ("Описание пятен, наблюдавшихся на Солнце, и их видимого вращения вместе с Солнцем"). Эту работу можно считать первым наблюдательным доказательством вращения Солнца. Христофор Шейнер (“Rosa Ursine sive solis”, book 4, part 2, 1630) был первым, кто измерил скорость вращения Солнца на экваторе и заметил, что вращение на высоких широтах происходит с меньшей скоростью, чем на низких, поэтому Шейнера можно считать первооткрывателем дифференциального вращения Солнца.

Каждое измерение даёт немного отличающийся от предыдущих результат, что приводит к возникновению стандартной ошибки (указана после +/-). С. Джон (1918) был, вероятно, первым, кто собрал опубликованные оценки скорости вращения Солнца и пришёл к заключению, что объяснить различие результатов только ошибками наблюдателей и местными возмущениями на Солнце сложно; вероятно, различия возникают из-за вариаций скорости вращения. Hubrecht (1915) указал на то, что два полушария Солнца вращаются несколько по-разному. Изучение магнитографических данных дало синодический период, равный 26,24 суткам на экваторе и почти 38 суткам на полюсах.

Внутреннее вращение Солнца

Схема внутреннего вращения Солнца, показывающая дифференциальное вращение во внешней части конвективной зоны и почти равномерное вращение в зоне лучистого переноса. Переход между двумя областями называется тахоклином.

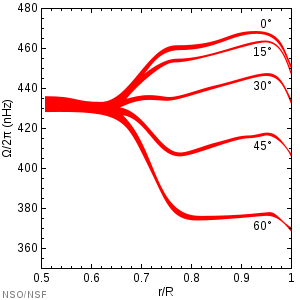
До эпохи гелиосейсмологии, исследования колебаний Солнца, о внутреннем вращении Солнца было известно очень мало. Предполагалось, что дифференциальный профиль вращения поверхности простирается на внутреннюю часть Солнца. По данным гелиосейсмологии известно, что вращение Солнца происходит не по этой схеме. Был получен профиль вращения; на поверхности Солнце медленнее вращается у полюсов и быстрее на экваторе. Такой механизм вращения существует и в конвективной зоне. В области тахоклина режим вращения резко меняется на твердотельное вращение в области лучистого переноса.

В 2021 году японский суперкомпьютер Фугаку точно смоделировать тепловую конвекцию и магнитное поле в недрах Солнца, которые в результате воспроизвели его дифференциальное вращение. Было достигнуто моделирование с беспрецедентно высоким разрешением. В симуляции использовались 5,4 миллиарда точек, и удалось воспроизвести дифференциальное вращение Солнца с быстрым экватором и медленными полюсами. На основе предыдущих расчетов предполагалось, что в зоне конвекции магнитная энергия меньше турбулентной и играет второстепенную роль. Однако теперь взгляд на недра Солнца изменился – модель показала сильные магнитные поля, энергия которых более чем в два раза превышает энергию турбулентности. Кроме этого, ученые выяснили, что магнитное поле играет важную роль в создании и поддержании дифференциального вращения Солнца.

Литература

• Cox, Arthur N., Ed. "Allen's Astrophysical Quantities", 4th Ed, Springer, 1999.
• Javaraiah, J., 2003. Long-Term Variations in the Solar Differential Rotation. Solar Phys., 212 (1): 23-49.
• St. John, C., 1918. The present condition of the problem of solar rotation, Publications of the Astronomical Society of the Pacific, V.30, No. 178, 318-325.

Ссылки

• Carrington Rotation Commencement Dates 1853-2016
• Carrington Rotation Start and Stop Times
• Carrington Rotation Number