Граф Клебша
| Граф Клебша | |
|---|---|
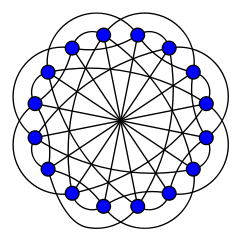 | |
| Вершин | 16 |
| Рёбер | 40 |
| Радиус | 2 |
| Диаметр | 2 |
| Обхват | 4 |
| Автоморфизмы | 1920 |
| Хроматическое число | 4[1] |
| Свойства |
Сильно регулярный Гамильтонов граф Граф без треугольников Граф Кэли Вершинно-транзитивен Рёберно-транзитивен Дистанционно-транзитивен |
В теории графов под графом Клебша понимается один из двух дополняющих друг друга графов, имеющих 16 вершин. Один из них имеет 40 рёбер и является 5-регулярным графом, другой имеет 80 рёбер и является 10-регулярным графом. 80-рёберный вариант — это половинный граф куба 5-го порядка. Назван графом Клебша в 1968 году Зайделем [2] ввиду его связи с конфигурацией прямых поверхности четвёртого порядка, открытой 1868 году немецким математиком Альфредом Клебшем. 40-рёберный вариант – это складной граф куба 5 порядка. Он известен также под именем граф Гринвуда — Глизона после работы Гринвуда и Глизона [3], в которой они использовали этот граф для вычисления числа Рамсея R (3,3,3) = 17[3] [4] [5].
Построение[править | править код]
Складной граф куба 5-го порядка (5-регулярный граф Клебша) может быть построен добавлением рёбер между противоположными вершинами графа 4-мерного гиперкуба (В n-мерном гиперкубе пара вершин противоположна, если кратчайшее расстояние между ними содержит n рёбер). Его можно построить также из графа 5-мерного гиперкуба стягиванием каждой пары противоположных вершин.
Ещё одно построение, дающее тот же граф, заключается в создании вершины для каждого элемента конечного поля GF (16) и соединении двух вершин ребром, если разность соответствующих элементов поля является кубом[6].
Половинный граф куба 5-го порядка (10-регулярный граф Клебша) — это дополнение 5-регулярного графа. Его можно также построить из вершин 5-мерного гиперкуба путём соединения пар вершин, между которыми расстояние Хэмминга равно точно двум. Это построение образует два подмножества по 16 вершин в каждом, не связанных друг с другом. Оба полученных графа изоморфны 10-регулярному графу Клебша.
Свойства[править | править код]
5-регулярный граф Клебша является сильно регулярным графом 5-й степени с параметрами [7][8]. Его дополнение, 10-регулярный граф Клебша, тоже сильно регулярен[1] [5].
5-регулярный граф Клебша является гамильтоновым, непланарным и не эйлеровым. Оба графа являются 5-вершинно связными и 5-рёберно связными. Подграф, порождённый десятью вершинами, не являющихся соседями какой-либо вершины в этом графе, изоморфен графу Петерсена.
Рёбра полного графа K16 можно разделить на три несвязных копии 5-регулярного графа Клебша. Поскольку граф Клебша не содержит треугольников, это показывает, что существует трёхцветное раскрашивание без треугольников рёбер графа K16. Таким образом, число Рамсея R (3,3,3), описывающее минимальное число вершин в полном графе при трёхцветном раскрашивании без треугольников, не может быть меньше 17. Гринвуд и Глизон использовали это построение как часть своего доказательства равенства R (3,3,3) = 17 [3][9].
5-регулярный граф Клебша является графом Келлера размерности два, и входит в семейство графов, используемых для поиска покрытия Евклидовых пространств большой размерности гиперкубами, не имеющими общих граней.
Алгебраические свойства[править | править код]
Характеристический многочлен 5-регулярного графа Клебша — это . Таким образом, граф Клебша является целым графом – его спектр состоит полностью из целых чисел[5]. Граф Клебша является единственным графом с таким характеристическим полиномом.
5-регулярный граф Клебша является графом Кэли c группой автоморфизмов порядка 1920, изоморфной группе Коксетера . Как в любом графе Кэли, группа автоморфизмов действует транзитивно на его вершины, делая его вершинно-транзитивным. Фактически он является симметричным графом, а потому он рёберно-транзитивен и дистанционно-транзитивен.
Галерея[править | править код]
-
Граф Клебша является гамильтоновым.
-
Ахроматическое число графа Клебша равно 8.
-
Хроматическое число графа Клебша равно 4.
-
Хроматический класс графа Клебша равен 5.
-
Конструирование графа Клебша из графа гиперкуба.
Примечания[править | править код]
- ↑ 1 2 . Eric W. Weisstein. Clebsch Graph. From MathWorld — A Wolfram Web Resource. Дата обращения: 13 августа 2009. Архивировано 7 февраля 2009 года.
- ↑ J. J. Seidel, Strongly regular graphs with (−1,1,0) adjacency matrix having eigenvalue 3, Lin. Alg. Appl. 1 (1968) 281—298.
- ↑ 1 2 3 R. E. Greenwood, Andrew Gleason. Combinatorial relations and chromatic graphs // Canadian Journal of Mathematics. — 1955. — Т. 7. — С. 1—7. — doi:10.4153/CJM-1955-001-4.
- ↑ A. Clebsch. Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen // J. für Math. — 1868. — Т. 69. — С. 142—184.
- ↑ 1 2 3 The Clebsch Graph on Bill Cherowitzo's home page. Дата обращения: 25 октября 2013. Архивировано 29 октября 2013 года.
- ↑ De Clerck, Frank Constructions and Characterizations of (Semi)partial Geometries. Summer School on Finite Geometries 6 (1997). Дата обращения: 25 октября 2013. Архивировано 15 июня 2011 года.
- ↑ Problems in algebraic combinatorics // Electronic Journal of Combinatorics. — 1995. — Т. 2. — С. 3.
- ↑ Peter J. Cameron Strongly regular graphs Архивная копия от 29 октября 2013 на Wayback Machine on DesignTheory.org, 2001
- ↑ Hugo S. Sun, M. E. Cohen. An easy proof of the Greenwood–Gleason evaluation of the Ramsey number R (3,3,3) // The Fibonacci Quarterly. — 1984. — Т. 22, вып. 3. — С. 235—238.
Для улучшения этой статьи желательно:
|




![Ахроматическое число[en] графа Клебша равно 8.](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d8/Complete_coloring_clebsch_graph.svg/120px-Complete_coloring_clebsch_graph.svg.png)


