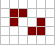
Натюрморт (конфигурация клеточного автомата)

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
У этого термина существуют и другие значения, см. Натюрморт (значения).

Натюрмо́рт — класс конфигураций в «Жизни» — созданной Конвеем модели клеточного автомата.

Описание[править | править код]

В наиболее общей формулировке понятие «натюрморт» означает то же, что и «устойчивая фигура» — конфигурация «Жизни» или другого клеточного автомата, которая не изменяется в процессе эволюции[nb 1]. Иными словами, натюрморт является осциллятором периода 1[1][2][3].

Терминология: натюрморты и псевдонатюрморты[править | править код]

Существует несколько близких по смыслу терминов, обозначающих не изменяющиеся в процессе эволюции конфигурации (конфигурации, являющиеся собственными родителями). Различия между ними связаны с ответом на следующие вопросы:

  1. Считается ли натюрмортом конфигурация, состоящая из двух независимых натюрмортов (например, двух блоков на достаточно большом расстоянии друг от друга)?[4]
  2. Считается ли натюрмортом конфигурация, состоящая из двух частей, любую из которых можно удалить так, что вторая часть продолжит существовать?

В существующих словарях и онлайн-энциклопедиях[3][5][6][7] приводятся следующие определения:

  • Устойчивый образец (англ. stable pattern) — объект, который является собственным родителем[1][2];
  • Натюрморт (англ. still life, strict still life) — устойчивый объект, являющийся конечным и непустым, из которого нельзя выделить непустую устойчивую часть[7][8][9];
  • Псевдонатюрморт (англ. pseudo still life) — устойчивый объект, не являющийся натюрмортом, в котором присутствует хотя бы одна мёртвая клетка, имеющая более трёх соседей всего, но меньше трёх соседей в каждом из содержащихся в объекте натюрмортов[7][10][11].

Точное определение «устойчивости» представляет интерес в контексте перечисления натюрмортов: например, согласно приведённым определениям, количество устойчивых конфигураций размера 8 (т.е. состоящих из 8 живых клеток) в «Жизни» бесконечно, так как пара блоков на любом расстоянии друг от друга является устойчивой; тем не менее, количество натюрмортов ограниченного размера считается конечным[5][6][7].

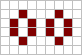Псевдонатюрморт в «Жизни». Удаление одного из островов не влияет на стабильность второго острова.
«Строгий» натюрморт. Стабильность каждого из островов зависит от наличия другого острова.

Известно число натюрмортов и псевдонатюрмортов размера не выше 24 клеток[7][10][11].

Задача определения типа устойчивой конфигурации (натюрморт, псевдонатюрморт) решается за полиномиальное время путём поиска циклов в связанном кососимметричном графе[12].

Натюрморты в «Жизни»[править | править код]

В «Жизни» существует множество естественных[13] натюрмортов.

Простые примеры[править | править код]

Блок[править | править код]

Наиболее распространённый натюрморт — блок[14][15][16] — конфигурация в форме квадрата 2 × 2. Два блока, размещённые в прямоугольнике 2 × 5, образуют би-блок — простейший псевдонатюрморт. Блоки используются в качестве составных частей во множестве сложных устройств, например, в планерном ружье Госпера[16].

Блок
Би-блок

Улей[править | править код]

Второй по распространённости натюрморт — улей (англ. hive, beehive). Ульи часто возникают четвёрками в конфигурации, называемой па́секой (англ. honey farm)[14][15][16].

Улей
Па́сека

Каравай[править | править код]

Третий по распространённости натюрморт — каравай (англ. loaf). Караваи нередко появляются парами (англ. bi-loaf)[14][15][16]. В свою очередь, двойные караваи также появляются в парах, называемых пека́рнями (англ. bakery)[17].

Каравай
Двойной каравай
Пекарня

Ящики, баржи, лодки, корабли[править | править код]

Ящик (англ. tub) состоит из четырёх живых клеток в окрестности фон Неймана центральной мёртвой клетки. Добавление одной живой клетки по диагонали к центральной клетке превращает ящик в лодку (англ. boat), а добавление симметрично ещё одной клетки — в корабль (англ. ship)[18]. Естественное удлинение этих трёх конфигураций даёт баржу (англ. barge), длинную лодку (англ. long-boat) и длинный корабль (англ. long-ship) соответственно. Удлинение можно продолжать сколь угодно долго[5][6][15][16].

Слева направо: ящик, баржа, длинная баржа, ...
Слева направо: лодка, длинная лодка, ...
Слева направо: корабль, длинный корабль, ...

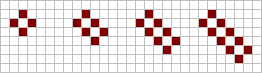Из двух лодок можно составить ещё один натюрморт — лодочный бант (англ. boat tie), а из двух кораблей — корабельный бант (англ. ship tie)[5][6].

Лодочный бант
Корабельный бант

Другие натюрморты[править | править код]

  • Каноэ
    Каноэ
  • Авианосец
    Авианосец
  • Знак интеграла
    Знак интеграла
  • Манго / Сигара
    Манго / Сигара
  • Пруд
    Пруд
  • Змея
    Змея

Пожиратели и отражатели[править | править код]

См. также: Отражатель (конфигурация клеточного автомата)

Натюрморты можно использовать для модификации или разрушения других объектов. Пожиратель (англ. eater) способен уничтожить космический корабль и восстановиться после реакции. Отражатель (англ. reflector) вместо уничтожения космического корабля изменяет направление его полёта.

Отражатели и пожиратели не обязательно должны являться натюрмортами.

  • Пожиратели
  • Рыболовный крючок / пожиратель-1
    Рыболовный крючок / пожиратель-1
  • Пожиратель-2
    Пожиратель-2

Максимальная плотность[править | править код]

Задача размещения в области n × n натюрморта с максимальным числом клеток привлекала к себе внимание программистов как задача программирования в ограничениях[19][20][21][22][23]. При стремлении размера области к бесконечности живыми могут быть не более 50% клеток[24]. На конечных квадратных областях можно достичь больших плотностей. Так, максимальная плотность натюрморта в квадрате 8 × 8 равна 36/64 = 0.5625 — эту плотность обеспечивает образец, состоящий из девяти блоков[19] Для квадратов до 20 × 20 известны оптимальные решения[25][26].

  • Натюрморты максимальной плотности в «Жизни»
  • 19x19
    19x19
  • 20x20
    20x20

Число натюрмортов[править | править код]

Число натюрмортов и псевдонатюрмортов в «Жизни» известно до размера в 24 клетки[27][28][29].

Число живых клеток Число натюрмортов Примеры
1 0
2 0
3 0
4 2 блок, ящик
5 1 лодка
6 5 баржа, авианосец, улей, корабль, змея
7 4 рыболовный крючок, каравай, длинная лодка
8 9 каноэ, манго, длинная баржа, пруд
9 10 знак интеграла
10 25 лодочный бант
11 46
12 121 корабельный бант
13 240
14 619 двойной каравай
15 1353
16 3286
17 7773
18 19044
19 45759 пожиратель 2
20 112243
21 273188
22 672172
23 1646147
24 4051711

Сноски[править | править код]

  1. ↑ Более строгие определения см. в разделе «Терминология».

Примечания[править | править код]

  1. ↑ 1 2 Устойчивый. Словарь Жизни. Дата обращения: 11 августа 2013. Архивировано 10 февраля 2013 года.
  2. ↑ 1 2 Stable. Life Lexicon. Дата обращения: 11 августа 2013. Архивировано из оригинала 20 февраля 2009 года.
  3. ↑ 1 2 Eric Weisstein. Still Life. Treasure Trove of Life C.A.. Дата обращения: 11 августа 2013. (недоступная ссылка)
  4. ↑ Если ответ на этот вопрос положительный, то количество натюрмортов с ограниченным числом клеток бесконечно.
  5. ↑ 1 2 3 4 Николай Белюченко. Словарь Жизни. Архивировано 10 октября 2012 года.
  6. ↑ 1 2 3 4 Stephen A. Silver. Life Lexicon (англ.). Архивировано 26 мая 2013 года.
  7. ↑ 1 2 3 4 5 Still life. ConwayLife.com. Дата обращения: 11 августа 2013. Архивировано 30 июля 2013 года.
  8. ↑ Натюрморт. Словарь Жизни. Дата обращения: 11 августа 2013. Архивировано 10 февраля 2013 года.
  9. ↑ Still life. Life Lexicon. Дата обращения: 11 августа 2013. Архивировано из оригинала 20 февраля 2009 года.
  10. ↑ 1 2 Псевдонатюрморт. Словарь Жизни. Дата обращения: 11 августа 2013. Архивировано 6 мая 2019 года.
  11. ↑ 1 2 Pseudo still life. Life Lexicon. Дата обращения: 11 августа 2013. Архивировано из оригинала 3 декабря 2014 года.
  12. ↑ Cook, Matthew (2003). "Still life theory". New Constructions in Cellular Automata. Santa Fe Institute Studies in the Sciences of Complexity, Oxford University Press. pp. 93—118.
  13. ↑ Естественный образец — объект, относительно часто возникающий в процессе развития случайной конфигурации.
  14. ↑ 1 2 3 Achim Flammenkamp. Top 100 of Game-of-Life Ash Objects. Дата обращения: 5 ноября 2008. Архивировано 22 октября 2008 года.
  15. ↑ 1 2 3 4 Игра Жизнь (обзор Гарднера). Дата обращения: 11 августа 2013. Архивировано 18 октября 2012 года.
  16. ↑ 1 2 3 4 5 Клумова И. Н. Игра «Жизнь» // Квант. — 1974. — № 9. — С. 26—30. Архивировано 4 марта 2016 года.
  17. ↑ Пекарня. Словарь Жизни. Дата обращения: 11 августа 2013. Архивировано 6 мая 2019 года.
  18. ↑ Не путать с космическим кораблём.
  19. ↑ 1 2 Bosch, R. A. Integer programming and Conway’s game of Life (неопр.) // SIAM Review. — 1999. — Т. 41, № 3. — С. 594—604. — doi:10.1137/S0036144598338252..
  20. ↑ Bosch, R. A. Maximum density stable patterns in variants of Conway’s game of Life (англ.) // Operations Research Letters  (англ.) (рус. : journal. — 2000. — Vol. 27, no. 1. — P. 7—11. — doi:10.1016/S0167-6377(00)00016-X..
  21. ↑ Smith, Barbara M. Principles and Practice of Constraint Programming - CP 2002 (англ.) : journal. — Springer-Verlag, 2002. — Vol. 2470. — P. 89—94. — doi:10.1007/3-540-46135-3_27..
  22. ↑ Bosch, Robert; Trick, Michael. Constraint programming and hybrid formulations for three Life designs (англ.) // Annals of Operations Research  (англ.) (рус. : journal. — 2004. — Vol. 130, no. 1—4. — P. 41—56. — doi:10.1023/B:ANOR.0000032569.86938.2f..
  23. ↑ Cheng, Kenil C. K.; Yap, Roland H. C. Applying ad-hoc global constraints with the case constraint to still-life (англ.) // Constraints : journal. — 2006. — Vol. 11, no. 2—3. — P. 91—114. — doi:10.1007/s10601-006-8058-9..
  24. ↑ Elkies, Noam D. (1998). "The still life density problem and its generalizations". Voronoi's Impact on Modern Science, Book I. Proc. Inst. Math. Nat. Acad. Sci. Ukraine, vol. 21. pp. 228—253. arXiv:math.CO/9905194.
  25. ↑ J. Larrosa, E. Morancho and D. Niso. On the Practical use of Variable Elimination in Constraint Optimization Problems: 'Still-life' as a Case Study (англ.) // Journal of Artificial Intelligence Research  (англ.) (рус. : journal. — 2005. — Vol. 23. — P. 421—440. Архивировано 16 июля 2011 года.
  26. ↑ Neil Yorke-Smith. Maximum Density Still Life. Artificial Intelligence Center. SRI International. Дата обращения: 11 августа 2013. Архивировано 19 мая 2013 года.
  27. ↑ Number of stable n-celled patterns («still lifes») in Conway's game of Life
  28. ↑ Number of n-celled pseudo-still-lifes in Conway's game of Life
  29. ↑ Niemiec, Mark D. Life Still-Lifes. Архивировано 21 января 2013 года.

Внешние ссылки[править | править код]

Источник — https://wiki4.ru/w/index.php?title=Натюрморт_(конфигурация_клеточного_автомата)&oldid=134979502