Полный двудольный граф
Перейти к навигации
Перейти к поиску

автоморфизмы =
вершин =
рёбер =
хроматическое число = 2
хроматический индекс =
радиус =
диаметр =
обхват ==
спектр =
обозначение =
Полный двудольный граф (биклика) — специальный вид двудольного графа, у которого любая вершина первой доли соединена со всеми вершинами второй доли вершин.
Определение[править | править код]
Полный двудольный граф — это такой двудольный граф, что для любых двух вершин и , является ребром в . Полный двудольный граф с долями размера и обозначается как .
Примеры[править | править код]
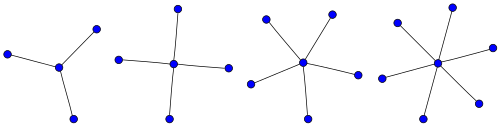

- Графы называются звёздами, все полные двудольные графы, являющиеся деревьями, являются звёздами.
- Граф называется клешнёй и используется для определения графов без клешней.
- Граф иногда называется «коммунальным графом», название восходит к классической задаче «домики и колодцы», в современной интерпретации использующей «коммунальную» формулировку (подключить три домика к водо-, электро- и газоснабжению без пересечений линий на плоскости); задача неразрешима ввиду непланарности графа .
Свойства[править | править код]
- Задача поиска для данного двудольного графа полного двудольного подграфа с заданным параметром NP-полна.
- Планарный граф не может содержать в качестве минора графа. Внешнепланарный граф не может содержать в качестве минора (Это не достаточное условие планарности и внешней планарности, а необходимое). И наоборот, любой непланарный граф содержит либо , либо полный граф в качестве минора (Теорема Понтрягина — Куратовского).
- Полные двудольные графы являются графами Мура и -клетками.
- Полные двудольные графы и являются графами Турана.
- Полный двудольный граф имеет размер вершинного покрытия, равный и размер рёберного покрытия, равный .
- Полный двудольный граф имеет максимальное независимое множество размером .
- Матрица смежности полного двудольного графа имеет собственные значения , и с кратностями , и соответственно.
- Матрица Лапласа полного двудольного графа имеет собственные значения , , , с кратностями , , и соответственно.
- Полный двудольный граф имеет остовных деревьев.
- Полный двудольный граф имеет максимальное паросочетание размера .
- Полный двудольный граф имеет подходящую -рёберную раскраску, соответствующую латинскому квадрату.
Последние два результата являются следствием теоремы Холла, применённой к -регулярному двудольному графу.
См. также[править | править код]
Литература[править | править код]
- John Adrian Bondy, U. S. R. Murty. Graph Theory with Applications. — North-Holland, 1976. — С. 5. — ISBN 0-444-19451-7. Архивировано 13 апреля 2010 года.
- Reinhard Diestel. Graph Theory // 3rd. — Springer, 2005. — С. 17. — ISBN 3-540-26182-6.
Для улучшения этой статьи желательно:
|









































