Преобразование Хафа

Преобразование Хафа (англ. Hough Transform) — вычислительный алгоритм, применяемый для параметрической идентификации геометрических элементов растрового изображения (патент 1962 г. Поля Хафа). Используется в анализе изображений, цифровой обработке изображений и компьютерном зрении. Предназначен для поиска объектов, принадлежащих определённому классу фигур, с использованием процедуры голосования. Процедура голосования применяется к пространству параметров, из которого и получаются объекты определённого класса фигур по локальному максимуму в так называемом накопительном пространстве (accumulator space), которое строится при вычислении трансформации Хафа.

Классический алгоритм преобразования Хафа связан с идентификацией прямых в изображении, но позже алгоритм был расширен возможностью идентификации позиции произвольной фигуры, чаще всего эллипсов и окружностей. Преобразование Хафа в том виде, котором оно используется теперь, было изобретено в 1981 году. Этот алгоритм назвали «обобщённым преобразованием Хафа» и его предложил Дана Баллард.

Теория

При автоматизированном анализе цифровых изображений очень часто возникает проблема идентификации простых фигур, таких как прямые, круги или эллипсы. Во многих случаях используется алгоритм поиска границ в качестве предобработки для получения точек, находящихся на кривой в изображении. Однако, либо из-за зашумлённости изображения, либо из-за несовершенства алгоритма обнаружения границ, могут появиться «потерянные» точки на кривой, также как и небольшие отклонения от идеальной формы прямой, круга или эллипса. По этим причинам часто довольно сложно приписать найденные границы соответствующим прямым, кругам и эллипсам в изображении. Назначение преобразования Хафа — разрешить проблему группировки граничных точек путём применения определённой процедуры голосования к набору параметризованных объектов изображения.

В простейшем случае преобразование Хафа является линейным преобразованием для обнаружения прямых. Прямая может быть задана уравнением y = mx + b и может быть вычислена по любой паре точек (x, y) на изображении. Главная идея преобразования Хафа — учесть характеристики прямой не как уравнение, построенное по паре точек изображения, а в терминах её параметров, то есть m — углового коэффициента и b — точки пересечения с осью ординат. Исходя из этого прямая, заданная уравнением y = mx + b, может быть представлена в виде точки с координатами (b, m) в пространстве параметров.

Однако прямые, параллельные оси ординат, имеют бесконечные значения для параметра m. Поэтому удобней представить прямую с помощью других параметров, известных как $r$ и $\theta$ [rho, theta]. Параметр $r$ — это длина радиус-вектора ближайшей к началу координат точки на прямой (то есть нормали к прямой, проведенной из начала координат), а $\theta$ — это угол между этим вектором и осью абсцисс. При таком описании прямых не возникают бесконечные параметры.

Таким образом, уравнение прямой можно записать как

$y=\left(-{\cos \theta \over \sin \theta }\right)x+\left({r \over {\sin \theta }}\right)$,

или после преобразования

$r=x\cos \theta +y\sin \theta$.

Поэтому возможно связать с каждой прямой на исходном изображении (в плоскости X-Y) точку с координатами r, θ в плоскости параметров, которая является уникальной при условии, что $\theta \in [0,\pi ]$ и $r\in \mathbf {R}$, или что $\theta \in [0,2\pi ]$ и $r\geq 0$.

Плоскость (r,θ) иногда называется Пространством Хафа для множества прямых в 2-мерном случае. Преобразование Хафа концептуально очень близко к 2-мерному преобразованию Радона (Radon transform) и может рассматриваться как его дискретное представление.

Через каждую точку плоскости может проходить бесконечно много прямых. Если эта точка имеет координаты $(x_{0},y_{0})$ , то все прямые, проходящие через неё, соответствуют уравнению:

$r(\theta )=x_{0}\cdot \cos \theta +y_{0}\cdot \sin \theta$.

Это соответствует синусоидальной линии в пространстве Хафа (r, θ), которая, в свою очередь, уникальна для данной точки и однозначно её определяет. Если эти линии (кривые), соответствующие двум точкам, накладываются друг на друга, то точка (в пространстве Хафа), где они пересекаются, соответствует прямым (в оригинальном месте изображения), которые проходят через обе точки. В общем случае, ряд точек, которые формируют прямую линию, определяют синусоиды, которые пересекаются в точке параметров для той линии. Таким образом, проблема обнаружения коллинеарных точек может быть сведена к проблеме обнаружения пересекающихся кривых.

Реализация

Алгоритм преобразования Хафа использует массив, называемый аккумулятором, для определения присутствия прямой y = mx + b. Размерность аккумулятора равна количеству неизвестных параметров пространства Хафа. Например, для линейной трансформации нужно использовать двумерный массив, так как имеются два неизвестных параметра: m и b. Два измерения аккумулятора соответствуют квантованным значениям параметров m и b. Для каждой точки и её соседей алгоритм определяет, достаточен ли вес границы в этой точке. Если да, то алгоритм вычисляет параметры прямой и увеличивает значение в ячейке аккумулятора, соответствующей данным параметрам.

Потом, найдя ячейки аккумулятора с максимальными значениями, обычно поиском локального максимума в пространстве аккумулятора, могут быть определены наиболее подходящие прямые. Самый простой способ — это пороговая фильтрация. Однако в разных ситуациях разные методы могут давать разные результаты. Так как полученные прямые не содержат информацию о длине, следующим шагом является нахождение частей изображения, соответствующих найденным прямым. Более того, из-за ошибок на этапе определения границ фигур в пространстве аккумулятора также будут содержаться ошибки. Это делает поиск подходящих линий нетривиальным.

Пример

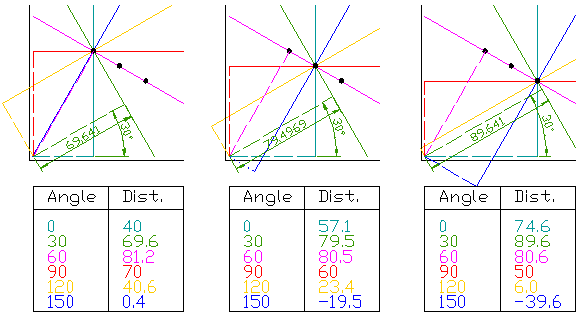
Рассмотрим исходное тестовое изображение из трех черных точек. Проверим, расположены ли точки на прямой линии.

• Через каждую точку проведено (для наглядности) только по шесть прямых, имеющих разный угол.
• К каждой прямой из начала координат построен перпендикуляр.
• Для всех прямых длина соответствующего перпендикуляра и его угол с осью абсцисс сведены в таблицу.
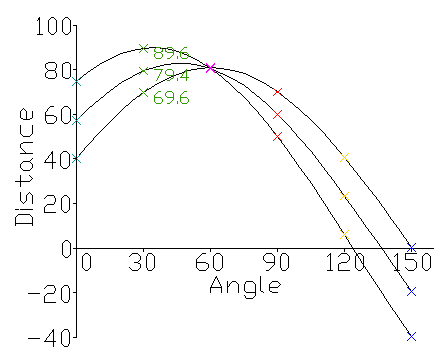
• Данные таблицы являются результатом преобразования Хафа и могут служить основой для графического представления в «пространстве Хафа».

Координаты точки пересечения синусоид определяют параметры прямой, общей для проверяемых точек на исходном изображении.

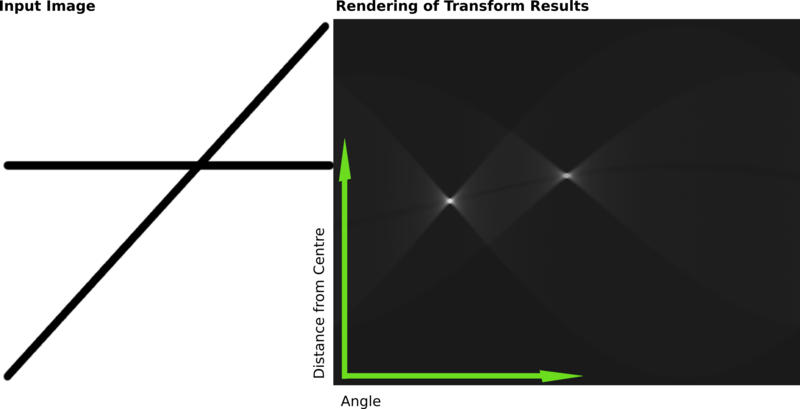
Следующий пример показывает результаты преобразования Хафа для изображения с двумя пересекающимися прямыми.

Результаты этого преобразования сохраняются в матрице. Значения в ячейках матрицы представляют собой количество кривых, проходящих через точку. Максимальные значения в ячейках соответствуют двум более ярким точкам на изображении и параметрам соответствующих прямых. Два ярких пятна — пересечения кривых двух линий. По этим пятнам можно определить угол и расстояние до прямой на исходном изображении.

Ограничения

Преобразование Хафа эффективно только при значительном количестве «попаданий» в соответствующий элемент пространства Хафа, только тогда можно с уверенностью определить фигуру, пренебрегая фоновым шумом. Это значит, что размер элемента не должен быть очень маленьким, иначе некоторые значения попадут в соседние элементы, уменьшая видимость нужного элемента.

Также, когда число параметров большое (больше трёх), среднее количество «попаданий» в элемент невелико, и поэтому верный элемент не будет очень сильно отличаться от соседей. Таким образом, алгоритм должен использоваться с большой осторожностью, чтобы не определить что-то иное как прямые и круги.

Эффективность алгоритма в большой степени обусловлена качеством входных данных: границы фигур на этапе предобработки изображения должны быть четко определены. Использование преобразования Хафа на зашумленных изображениях затруднено. Для зашумленных изображений необходим этап предобработки с целью подавления шума. В случае, если изображение повреждено, спекл, как в случае с изображением с индикатора радара, для определения линий предпочтительнее преобразование Радона, так как оно имеет хороший эффект шумоподавления при суммировании.

См. также

• Быстрое преобразование Хафа
• Обобщённое преобразование Хафа
• Преобразование Радона
• Преобразование Фурье

Ссылки

• https://web.archive.org/web/20070827233423/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/Hough.html - Java Applet + Исходники для изучения трансформации по уравнению y = mx + b
• https://web.archive.org/web/20070827191440/http://www.rob.cs.tu-bs.de/content/04-teaching/06-interactive/HNF.html - Java Applet + Исходники для изучения трансформации по уравнению в нормальной форме
• http://homepages.inf.ed.ac.uk/rbf/HIPR2/hough.htm Архивная копия от 11 февраля 2021 на Wayback Machine
• http://robocraft.ru/blog/computervision/502.html Архивная копия от 9 мая 2011 на Wayback Machine - Преобразование Хафа в OpenCV