Тригонометрия

Тригономе́трия (от др.-греч. τρίγωνον «треугольник» и μετρέω «измеряю», то есть измерение треугольников) — раздел математики, в котором изучаются тригонометрические функции и их использование в геометрии. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, архитектуре и геодезии для вычисления одних элементов треугольника по данным о других его элементах.

Тригонометрические вычисления применяются практически во всех областях геометрии, физики и инженерного дела. Например, большое значение имеет техника триангуляции, позволяющая измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.

История

Основная статья: История тригонометрии

Древняя Греция

Древнегреческие математики в своих построениях, связанных с измерением дуг круга, использовали технику хорд. Перпендикуляр к хорде, опущенный из центра окружности, делит пополам дугу и опирающуюся на неё хорду. Половина поделенной пополам хорды — это синус половинного угла (для единичной окружности), и поэтому функция синус известна также как «половина хорды». Благодаря этой зависимости, значительное число тригонометрических тождеств и теорем, известных сегодня, были также известны древнегреческим математикам, но в эквивалентной хордовой форме. Хотя в работах Евклида и Архимеда нет тригонометрии в строгом смысле этого слова, их теоремы представлены в геометрическом виде, эквивалентном специфическим тригонометрическим формулам. Теорема Архимеда для деления хорд эквивалентна формулам для синусов суммы и разности углов. Для компенсации отсутствия таблицы хорд математики времен Аристарха иногда использовали хорошо известную теорему, в современной записи — sinα/sinβ < α/β < tgα/tgβ, где 0° < β < α < 90°, совместно с другими теоремами.

Первые тригонометрические таблицы были, вероятно, составлены Гиппархом Никейским (180—125 лет до н. э.). Гиппарх был первым, кто свёл в таблицы соответствующие величины дуг и хорд для серии углов. Систематическое использование полной окружности в 360° установилось в основном благодаря Гиппарху и его таблице хорд. Возможно Гиппарх взял идею такого деления у Гипсикла, который ранее разделил день на 360 частей, хотя такое деление дня могли предложить и вавилонские астрономы.

Менелай Александрийский (100 н. э.) написал «Сферику» в трёх книгах. В первой книге он представил основы для сферических треугольников, аналогично I книге «Начал» Евклида о плоских треугольниках. Он представил теорему, для которой нет аналога у Евклида, о том, что два сферических треугольника конгруэнтны, если соответствующие углы равны, но он не делал различия между конгруэнтными и симметричными сферическими треугольниками. Другая его теорема гласит о том, что сумма углов сферического треугольника всегда больше 180°. Вторая книга «Сферики» применяет сферическую геометрию к астрономии. Третья книга содержит «теорему Менелая», известную также как «правило шести величин».

Позднее Клавдий Птолемей (90 — 168 г. н. э.) в «Альмагесте» расширил Гиппарховы «Хорды в окружности». Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. Теорема, которая была центральной в вычислении хорд Птолемея, также известна сегодня как теорема Птолемея, которая говорит о том, что сумма произведений противоположных сторон выпуклого вписанного четырёхугольника равна произведению диагоналей. Отдельный случай теоремы Птолемея появился как 93-е предложение «Данных» Евклида.

Теорема Птолемея влечёт за собой эквивалентность четырёх формул суммы и разности для синуса и косинуса. Позднее Птолемей вывел формулу половинного угла. Птолемей использовал эти результаты для создания своих тригонометрических таблиц, хотя, возможно, эти таблицы были выведены из работ Гиппарха.

Средневековая Индия

Замена хорд синусами стала главным достижением средневековой Индии. Такая замена позволила вводить различные функции, связанные со сторонами и углами прямоугольного треугольника. Таким образом, в Индии было положено начало тригонометрии как учению о тригонометрических величинах.

Индийские учёные пользовались различными тригонометрическими соотношениями, в том числе и теми, которые в современной форме выражаются как

$\sin ^{2}\alpha +\cos ^{2}\alpha =1,$

$\sin \alpha =\cos(90^{\circ }-\alpha ),$

$\sin(\alpha \pm \beta )=\sin \alpha \cos \beta \pm \cos \alpha \sin \beta .$

Индийцы также знали формулы для кратных углов $\sin n\alpha ,\qquad \cos n\alpha ,$ где $n=2,3,4,5.$

Тригонометрия необходима для астрономических расчётов, которые оформляются в виде таблиц. Первая таблица синусов имеется в «Сурья-сиддханте» и у Ариабхаты. Позднее учёные составили более подробные таблицы: например, Бхаскара приводит таблицу синусов через 1°.

Южноиндийские математики в XVI веке добились больших успехов в области суммирования бесконечных числовых рядов. По-видимому, они занимались этими исследованиями, когда искали способы вычисления более точных значений числа π. Нилаканта словесно приводит правила разложения арктангенса в бесконечный степенной ряд. А в анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды. Нужно сказать, что в Европе к подобным результатам подошли лишь в 17-18 вв. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 г., а ряд арктангенса был найден Дж. Грегори в 1671 г. и Г. В. Лейбницем в 1673 г.

С VIII века учёные стран Ближнего и Среднего Востока развили тригонометрию своих предшественников. В середине IX века среднеазиатский учёный аль-Хорезми написал сочинение «Об индийском счёте». После того как трактаты мусульманских ученых были переведены на латынь, многие идеи греческих, индийских и мусульманских математиков стали достоянием европейской, а затем и мировой науки.

Определение тригонометрических функций

Основная статья: Тригонометрические функции

Тригонометрические функции угла θ внутри единичной окружности

Первоначально тригонометрические функции были связаны с соотношениями сторон в прямоугольном треугольнике. Их единственным аргументом является угол (один из острых углов этого треугольника).

• Синус — отношение противолежащего катета к гипотенузе.
• Косинус — отношение прилежащего катета к гипотенузе.
• Тангенс — отношение противолежащего катета к прилежащему.
• Котангенс — отношение прилежащего катета к противолежащему.
• Секанс — отношение гипотенузы к прилежащему катету.
• Косеканс — отношение гипотенузы к противолежащему катету.

Данные определения позволяют вычислить значения функций для острых углов, то есть от 0° до 90° (от 0 до $\pi \over 2$ радиан). В XVIII веке Леонард Эйлер дал современные, более общие определения, расширив область определения этих функций на всю числовую ось. Рассмотрим в прямоугольной системе координат окружность единичного радиуса (см. рисунок) и отложим от горизонтальной оси угол $\theta$ (если величина угла положительна, то откладываем против часовой стрелки, иначе по часовой стрелке). Точку пересечения построенной стороны угла с окружностью обозначим A. Тогда:

• Синус угла $\theta$ определяется как ордината точки A.
• Косинус — абсцисса точки A.
• Тангенс — отношение ординаты точки единичной окружности к её абсциссе, причём эта точка не принадлежит оси ординат.
• Котангенс — отношение абсциссы точки единичной окружности к её ординате, причём эта точка не принадлежит оси абсцисс.
• Секанс — величина, обратная косинусу.
• Косеканс — величина, обратная синусу.

Для острых углов новые определения совпадают с прежними.

Возможно также чисто аналитическое определение этих функций, которое не связано с геометрией и представляет каждую функцию её разложением в бесконечный ряд.

Свойства функции синус

Синус

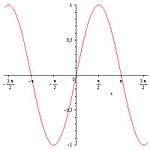
1. Область определения функции — множество всех действительных чисел: $D(y)=R$.
2. Множество значений — промежуток [−1; 1]: $E(y)$ = [−1;1].
3. Функция $y=\sin \left(\alpha \right)$ является нечётной: $\sin \left(-\alpha \right)=-\sin \alpha$.
4. Функция периодическая, наименьший положительный период равен $2\pi$: $\sin \left(\alpha +2\pi \right)=\sin \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha =\pi n\,,n\in \mathbb {Z}$.
6. Промежутки знакопостоянства: $y>0$ при $\left(2\pi n+0;\pi +2\pi n\right)\,,n\in \mathbb {Z}$ и $y<0$ при $\left(\pi +2\pi n;2\pi +2\pi n\right)\,,n\in \mathbb {Z}$.
7. Функция непрерывна и имеет производную при любом значении аргумента: $(\sin \alpha )'=\cos \alpha$
8. Функция $y=\sin \alpha$ возрастает при $\alpha \in \left(-{\frac {\pi }{2}}+2\pi n;{\frac {\pi }{2}}+2\pi n\right)\,,n\in \mathbb {Z}$, и убывает при $\alpha \in \left({\frac {\pi }{2}}+2\pi n;3{\frac {\pi }{2}}+2\pi n\right)\,,n\in \mathbb {Z}$.
9. Функция имеет минимум при $\alpha =-{\frac {\pi }{2}}+2\pi n\,,n\in \mathbb {Z}$ и максимум при $\alpha ={\frac {\pi }{2}}+2\pi n\,,n\in \mathbb {Z}$.

Свойства функции косинус

Косинус

1. Область определения функции — множество всех действительных чисел: $D(y)=R$.
2. Множество значений — промежуток [−1; 1]: $E(y)$ = [−1;1].
3. Функция $y=\cos \left(\alpha \right)$ является чётной: $\cos \left(-\alpha \right)=\cos \alpha$.
4. Функция периодическая, наименьший положительный период равен $2\pi$: $\cos \left(\alpha +2\pi \right)=\cos \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha ={\frac {\pi }{2}}+\pi n\,,n\in \mathbb {Z}$.
6. Промежутки знакопостоянства: $y>0$ при $\left(-{\frac {\pi }{2}}+2\pi n;{\frac {\pi }{2}}+2\pi n\right)\,,n\in \mathbb {Z}$ и $y<0$ при $\left({\frac {\pi }{2}}+2\pi n;3{\frac {\pi }{2}}+2\pi n\right)\,,n\in \mathbb {Z} .$
7. Функция непрерывна и имеет производную при любом значении аргумента: $(\cos \alpha )'=-\sin \alpha$
8. Функция $y=\cos \alpha$ возрастает при $\alpha \in \left(-\pi +2\pi n;2\pi n\right)\,,n\in \mathbb {Z} ,$ и убывает при $\alpha \in \left(2\pi n;\pi +2\pi n\right)\,,n\in \mathbb {Z} .$
9. Функция имеет минимум при $\alpha =\pi +2\pi n\,,n\in \mathbb {Z}$ и максимум при $\alpha =2\pi n\,,n\in \mathbb {Z} .$

Свойства функции тангенс

Тангенс

1. Область определения функции — множество всех действительных чисел: $D(y)=R$, кроме чисел $\alpha ={\frac {\pi }{2}}+\pi n,n\in \mathbb {Z} \,.$
2. Множество значений — множество всех действительных чисел: $E(y)=R.$
3. Функция $y=\mathrm {tg} \left(\alpha \right)$ является нечётной: $\mathrm {tg} \left(-\alpha \right)=-\mathrm {tg} \ \alpha$.
4. Функция периодическая, наименьший положительный период равен $\pi$: $\mathrm {tg} \left(\alpha +\pi \right)=\mathrm {tg} \left(\alpha \right)$.
5. График функции пересекает ось Ох при $\alpha =\pi n\,,n\in \mathbb {Z}$.
6. Промежутки знакопостоянства: $y>0$ при $\left(\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in \mathbb {Z}$ и $y<0$ при $\left(-{\frac {\pi }{2}}+\pi n;\pi n\right)\,,n\in \mathbb {Z}$.
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: $(\mathop {\operatorname {tg} } \,x)'={\frac {1}{\cos ^{2}x}}.$
8. Функция $y=\mathrm {tg} \ \alpha$ возрастает при $\alpha \in \left(-{\frac {\pi }{2}}+\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in \mathbb {Z}$.

Свойства функции котангенс

Котангенс

1. Область определения функции — множество всех действительных чисел: $D(y)=R,$ кроме чисел $\alpha =\pi n,n\in \mathbb {Z} \,.$
2. Множество значений — множество всех действительных чисел: $E(y)=R.$
3. Функция $y=\mathop {\operatorname {ctg} } \left(\alpha \right)$ является нечётной: $\mathop {\operatorname {ctg} } \left(-\alpha \right)=-\mathop {\operatorname {ctg} } \ \alpha \,.$
4. Функция периодическая, наименьший положительный период равен $\pi$: $\mathop {\operatorname {ctg} } \left(\alpha +\pi \right)=\mathop {\operatorname {ctg} } \left(\alpha \right).$
5. График функции пересекает ось Ох при $\alpha ={\frac {\pi }{2}}+\pi n\,,n\in \mathbb {Z} \,.$
6. Промежутки знакопостоянства: $y>0$ при $\left(\pi n;{\frac {\pi }{2}}+\pi n\right)\,,n\in \mathbb {Z}$ и $y<0$ при $\left({\frac {\pi }{2}}+\pi n;\pi \left(n+1\right)\right)\,,n\in \mathbb {Z} .$
7. Функция непрерывна и имеет производную при любом значении аргумента из области определения: $(\mathop {\operatorname {ctg} } \,x)'=-{\frac {1}{\sin ^{2}x}}.$
8. Функция $y=\mathop {\operatorname {ctg} } \ \alpha$ убывает при $\alpha \in \left(\pi n;\pi \left(n+1\right)\right)\,,n\in \mathbb {Z} .$

Применение тригонометрии

Секстант — навигационный измерительный инструмент, используемый для измерения высоты светила над горизонтом с целью определения географических координат той местности, в которой производится измерение.

Существует множество областей, в которых применяются тригонометрия и тригонометрические функции. Например, метод триангуляции используется в астрономии для измерения расстояния до ближайших звезд, в географии для измерения расстояний между объектами, а также в спутниковых навигационных системах. Синус и косинус имеют фундаментальное значение для теории периодических функций, например при описании звуковых и световых волн.

Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов, когда требуется сферическая тригонометрия), в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятностей, в статистике, в биологии, в медицинской визуализации (например, компьютерная томография и ультразвук), в аптеках, в химии, в теории чисел (следовательно, и в криптологии), в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях.

Стандартные тождества

Тождества — это равенства, справедливые при любых допустимых значениях входящих в них переменных.

$\sin ^{2}A+\cos ^{2}A=1\ .$

$\sec ^{2}A-{\mathop {\operatorname {tg} } }^{2}A=1\ .$

$\csc ^{2}A-{\mathop {\operatorname {ctg} } }^{2}A=1\ .$

Формулы преобразования суммы углов

$\sin(A\pm B)=\sin A\ \cos B\pm \cos A\ \sin B.$

$\cos(A\pm B)=\cos A\ \cos B\mp \sin A\ \sin B.$

$\mathop {\operatorname {tg} } (A\pm B)={\frac {\mathop {\operatorname {tg} } A\pm \mathop {\operatorname {tg} } B}{1\mp \mathop {\operatorname {tg} } A\ \mathop {\operatorname {tg} } B}}.$

$\mathop {\operatorname {ctg} } (A\pm B)={\frac {\mathop {\operatorname {ctg} } A\ \mathop {\operatorname {ctg} } B\mp 1}{\mathop {\operatorname {ctg} } B\pm \mathop {\operatorname {ctg} } A}}.$

Общие формулы

Треугольник со сторонами a, b, c и соответственно противоположными углами A, B, C

В следующих тождествах A, B и C являются углами треугольника; a, b, c — длины сторон треугольника, лежащие напротив соответствующих углов.

Теорема синусов

Стороны треугольника пропорциональны синусам противолежащих углов. Для произвольного треугольника

${\frac {a}{\sin A}}={\frac {b}{\sin B}}={\frac {c}{\sin C}}=2R,$

где $R$ — радиус окружности, описанной вокруг треугольника.

$R={\frac {abc}{\sqrt {(a+b+c)(a-b+c)(a+b-c)(b+c-a)}}}.$

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$c^{2}=a^{2}+b^{2}-2ab\cos C,$

или:

$\cos C={\frac {a^{2}+b^{2}-c^{2}}{2ab}}.$

Теорема тангенсов

${\frac {a-b}{a+b}}={\frac {\mathop {\operatorname {tg} } \left[{\tfrac {1}{2}}(A-B)\right]}{\mathop {\operatorname {tg} } \left[{\tfrac {1}{2}}(A+B)\right]}}$

Формула Эйлера

Формула Эйлера утверждает, что для любого действительного числа $x$ выполнено следующее равенство:

$e^{ix}=\cos x+i\sin x,$

где $e$ — основание натурального логарифма, $i$ — мнимая единица. Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:

$\cos x=\mathrm {Re} \{e^{ix}\}={e^{ix}+e^{-ix} \over 2},$

$\sin x=\mathrm {Im} \{e^{ix}\}={e^{ix}-e^{-ix} \over 2i}.$

Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:

$e^{ix}=\cos x+i\sin x\;,$

$e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;.$

с последующим решением относительно синуса или косинуса.

Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:

$\cos iy={e^{-y}+e^{y} \over 2}=\operatorname {ch} y,$

$\sin iy={e^{-y}-e^{y} \over 2i}=-{1 \over i}{e^{y}-e^{-y} \over 2}=i\operatorname {sh} y.$

Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением.

Решение простых тригонометрических уравнений

• $\sin x=a.$

Если $|a|>1$ — вещественных решений нет.

Если $|a|\leqslant 1$ — решением является число вида $x=(-1)^{n}\arcsin a+\pi n;\ n\in \mathbb {Z} .$

• $\cos x=a.$

Если $|a|>1$ — вещественных решений нет.

Если $|a|\leqslant 1$ — решением является число вида $x=\pm \arccos a+2\pi n;\ n\in \mathbb {Z} .$

• $\operatorname {tg} \,x=a.$

Решением является число вида $x=\operatorname {arctg} \,a+\pi n;\ n\in \mathbb {Z} .$

• $\operatorname {ctg} \,x=a.$

Решением является число вида $x=\operatorname {arcctg} \,a+\pi n;\ n\in \mathbb {Z} .$

Сферическая тригонометрия

Основная статья: Сферическая тригонометрия

Важным частным разделом тригонометрии, используемым в астрономии, геодезии, навигации и других отраслях, является сферическая тригонометрия, рассматривающая свойства углов между большими кругами на сфере и дуг этих больших кругов. Геометрия сферы существенно отличается от евклидовой планиметрии; так, сумма углов сферического треугольника, вообще говоря, отличается от 180°, треугольник может состоять из трёх прямых углов. В сферической тригонометрии длины сторон треугольника (дуги больших кругов сферы) выражаются посредством центральных углов, соответствующих этим дугам. Поэтому, например, сферическая теорема синусов выражается в виде

${\frac {\sin a}{\sin A}}={\frac {\sin b}{\sin B}}={\frac {\sin c}{\sin C}},$

и существуют две теоремы косинусов, двойственные друг другу.

См. также

• Гониометрия — раздел тригонометрии, где изучаются способы измерения углов, свойства тригонометрических функций и соотношения между ними.
• Решение треугольников
• Тригонометрические тождества
• Тригонометрические функции

Литература

• Boyer, Carl B. A History of Mathematics (англ.). — Second Edition. — John Wiley & Sons, Inc., 1991. — ISBN 0-471-54397-7.
• Christopher M. Linton (2004). From Eudoxus to Einstein: A History of Mathematical Astronomy. Cambridge University Press.
• Weisstein, Eric W. «Trigonometric Addition Formulas». Wolfram MathWorld. Weiner.