Мировая линия

Мировая линия объекта — это путь объекта в 4-мерном пространстве-времени. Это важное понятие в современной физике, и в особенности в теоретической физике.

Концепция «мировой линии» отличается от таких понятий, как «орбита» или «траектория» (например, орбита планеты в космосе или траектория автомобиля на дороге) наличием измерения времени и обычно охватывает большую область пространства-времени, в которой воспринимаемые прямые пути пересчитываются так, чтобы показать их (относительно) более абсолютные состояния положений для раскрытия природы специальной теории относительности или гравитационных взаимодействий.

Идея мировых линий зародилась в физике и была предложена Германом Минковским. Этот термин сейчас чаще всего используется в теориях относительности (то есть специальной теории относительности и общей теории относительности).

Использование в физике

В физике мировая линия объекта (упрощенного до точки в пространстве, например, частица или наблюдатель) — это последовательность пространственно-временных событий, соответствующая истории объекта. Мировая линия — это особый тип кривой в пространстве-времени. Ниже будет объяснено эквивалентное определение: Мировая линия — это времениподо́бная кривая в пространстве-времени. Каждая точка мировой линии — это событие, которое может быть отмечено временем и пространственным положением объекта в это время.

Например, орбита Земли в космосе представляет собой приблизительно круг, трехмерную (замкнутую) кривую в космосе: Земля каждый год возвращается в одну и ту же точку в космосе относительно Солнца. Однако она прибывает туда в другое (позднее) время. Мировая линия Земли спиральна в пространстве-времени (кривая в четырёхмерном пространстве) и не возвращается в ту же точку.

Пространство-время — это совокупность точек, называемых событиями, вместе с непрерывной и гладкой системой координат, определяющей события. Каждое событие может быть помечено четырьмя числами: координатой времени и тремя пространственными координатами; таким образом, пространство-время — это четырёхмерное пространство. Математический термин для пространства-времени — это четырёхмерное многообразие . Концепция может быть применена также к пространству более высоких измерений. Для упрощения четырёхмерной визуализации две пространственные координаты часто опускаются. Событие представляется точкой на диаграмме Минковского, которая представляет собой плоскость, с нанесенной вверх временной координатой, например $t$, и горизонтальной пространственной координатой, например $x$. По выражению Ф. Р. Харви

Кривая M в [пространстве-времени] называется мировой линией частицы, если её касательная в каждой точке времениподобна в будущем. Параметр длины дуги называется собственным временем и обычно обозначается как τ. Длина M называется собственным временем мировой линии или частицы. Если мировая линия M является отрезком прямой, то говорят, что частица находится в свободном падении.

Мировая линия очерчивает путь единственной точки в пространстве-времени. Мировой лист — это аналогичная двумерная поверхность, очерченная одномерной линией (например, струной), перемещающейся в пространстве-времени. Мировой лист открытой струны (со свободными концами) — полоса; замкнутая струна (петля) напоминает трубку.

Как только объект не упрощается до простой точки, а имеет объём, он очерчивает не мировую линию, а скорее мировую трубу.

Мировые линии как инструмент описания событий

Мировая линия, мировой лист и мировой объём получены из частиц, струн и бран .

Одномерная линия или кривая могут быть представлены координатами как функцией одного параметра. Каждое значение параметра соответствует точке в пространстве-времени, и варьирование параметра позволяет очертить линию. Таким образом, с математической точки зрения кривая определяется четырьмя координатными функциями $x^{a}(\tau ),\;a=0,1,2,3$ (где $x^{0}$ обычно обозначает временную координату) в зависимости от одного параметра $\tau$. Координатная сетка в пространстве-времени — это набор кривых, которые можно получить, если три из четырёх координатных функций взяты за константу.

Иногда термин мировая линия свободно используется для обозначения любой кривой в пространстве-времени. Эта терминология вызывает недоумение. Точнее, мировая линия — это кривая в пространстве-времени, которая отслеживает (временную) историю частицы, наблюдателя или небольшого объекта. Обычно в качестве параметра $\tau$ кривой берется собственное время объекта или наблюдателя по мировой линии.

Тривиальные примеры кривых в пространстве-времени

Три разные мировые линии изображают путешествие с разными постоянными четырёмя скоростями. t — время и x расстояние.

Кривая, состоящая из горизонтального отрезка (линия с постоянной координатой времени), может представлять стержень в пространстве-времени и не будет мировой линией в собственном смысле. Параметр отслеживает длину стержня.

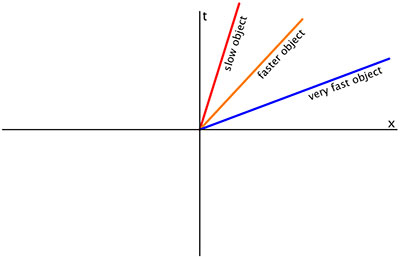
Линия с постоянной пространственной координатой (вертикальная линия в принятом выше соглашении) может представлять частицу в состоянии покоя (или неподвижного наблюдателя). Наклонная линия представляет частицу с постоянной координатной скоростью (постоянное изменение пространственной координаты с увеличением временной координаты). Чем больше линия отклонена от вертикали, тем больше скорость частицы.

Две мировые линии, которые начинаются раздельно а затем пересекаются, означают столкновение или «встречу». Две мировые линии, начинающиеся в одном и том же событии в пространстве-времени, каждая из которых впоследствии следует своим путем, могут представлять распад частицы на две другие или испускание одной частицы другой.

Мировые линии частицы и наблюдателя могут быть связаны с мировой линией фотона (путь света) и образовывать диаграмму, изображающую испускание фотона частицей, который впоследствии наблюдается наблюдателем (или поглощается другой частицей).

Мировые линии в специальной теории относительности

До сих пор мировая линия (и концепция касательных векторов) описывалась без средств количественной оценки интервала между событиями. Базовая математика такова: специальная теория относительности накладывает некоторые ограничения на возможные мировые линии. В специальной теории относительности описание пространства-времени ограничено специальными системами координат, которые не ускоряются (а значит, и не вращаются), называемыми инерциальными системами координат . В таких системах координат скорость света постоянна. Структура пространства-времени определяется билинейной формой η, которая дает действительное число для каждой пары событий. Билинейную форму иногда называют метрикой пространства-времени, но поскольку отдельные события иногда приводят к нулевому её значению, в отличие от метрик в метрических пространствах математики, билинейная форма не является математической метрикой пространства-времени.

Мировые линии свободно падающих частиц/объектов называются геодезическими . В специальной теории относительности это прямые линии в пространстве Минковского .

Часто единицы времени выбираются так, что скорость света представлена линиями под фиксированным углом, обычно под углом 45 градусов, образуя конус с вертикальной (временной) осью. Полезные кривые в пространстве-времени могут быть трех типов (другие типы будут частично одним, частично другим типом):

• светоподобные кривые, имеющие в каждой точке скорость света. Они образуют конус в пространстве-времени, разделяя его на две части. Конус является трехмерным в пространстве-времени, на чертежах он отображается как линия с двумя скрытыми измерениями, и как конус на чертежах с одним скрытым пространственным измерением.

Пример светового конуса, трехмерная поверхность всех возможных световых лучей, приходящих и исходящих из точки пространства-времени. Здесь он изображен с одним скрытым пространственным измерением.

Мгновенно сопутствующие инерциальные системы отсчета вдоль траектории («мировой линии») быстро ускоряющегося наблюдателя (в центре). Вертикальное направление отображает время, в то время как горизонтальное отображает расстояние, пунктирная линия — пространство-время наблюдателя. Маленькие точки — это определённые события в пространстве-времени. Обратите внимание на то, как изменяется мгновенно сопутствующая инерциальная система отсчета при ускорении наблюдателя.

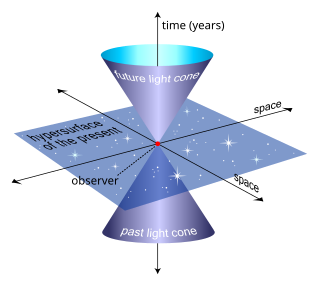
• времениподобные кривые, со скоростью меньше скорости света. Эти кривые должны попадать в конус, обозначенный светоподобными кривыми. В нашем определении выше: мировые линии — это времениподобные кривые в пространстве-времени .
• пространственноподобные кривые, выходящие за пределы светового конуса. Такие кривые могут описывать, например, длину физического объекта. Окружность цилиндра и длина стержня представляют собой пространственные кривые.

В любом заданном событии мировой линии пространство-время (пространство Минковского) делится на три части.

• Будущее данного события формируется всеми событиями, которые могут быть достигнуты через времениподобные кривые, лежащие в пределах светового конуса будущего.
• Прошлое данного события формируется всеми событиями, которые могут повлиять на это событие (то есть, которые могут быть связаны мировыми линиями в пределах светового конуса прошлого с данным событием).
  • Световой конус данного события формируется всеми событиями, которые могут быть связаны через световые лучи с этим событием. Когда мы наблюдаем ночное небо, мы, по сути, видим только световой конус прошлого во всем пространстве-времени.
• Прочая область находится между двумя световыми конусами. Точки в прочей области выбранного наблюдателя ему/ей недоступны; только точки в прошлом могут посылать сигналы данному наблюдателю. В обычном лабораторном опыте, используя общие единицы и методы измерения, может казаться, что мы смотрим на настоящее, тогда как на самом деле всегда есть задержка распространения света. Например, мы видим Солнце таким, каким оно было около 8 минут назад, а не таким, каким оно является «сейчас». В отличие от настоящего в теории Галилея/Ньютона, прочая область довольно толстая; это не 3-мерный объём, а 4-мерная область пространства-времени.
  • В «прочую область» входит гиперплоскость одновременности, которая определяется для данного наблюдателя пространством, которое гиперболически-ортогонально его мировой линии. Гиперплоскость одновременности трехмерная, хотя на схеме это будет 2-плоскость, потому что нам пришлось отбросить одно измерение, чтобы сделать картину более понятной. Хотя световые конусы одинаковы для всех наблюдателей в данном пространственно-временном событии, разные наблюдатели с разными скоростями, но находящиеся в одном событии (точке) в пространстве-времени, имеют пересекающие под углом друг друга мировые линии. Угол между этими линиями определяется относительными скоростями наблюдателей, и, следовательно, наблюдатели имеют разные гиперплоскости одновременности.
  • Настоящее часто означает единичное выбранное пространственно-временное событие.

Гиперплоскость одновременности

Мировая линия $w(\tau )\in R^{4}$ определяет 4-вектор скорости $v={\frac {dw}{d\tau }}$ который времениподобен. Форма Минковского $\eta (v,x)$ определяет линейную функцию $R^{4}\rightarrow R$ от $x\mapsto \eta (v,x).$ Пусть N — нулевое пространство (англ. null space, см. также ядро в алгебре) этого линейного функционала. Тогда N называется гиперплоскостью одновременности относительно v. Относительность одновременности — это утверждение, что N зависит от v . В самом деле, N — ортогональное дополнение к v относительно η . Когда две мировые линии u и w связаны соотношением ${\frac {du}{d\tau }}={\frac {dw}{d\tau }},$ то они разделяют одну и ту же гиперплоскость одновременности. Эта гиперплоскость существует математически, но физические отношения в теории относительности включают перемещение информации при помощи света. Например, традиционная электростатическая сила, описываемая законом Кулона, может быть изображена в гиперплоскости одновременности, но релятивистские отношения заряда и силы включают запаздывающие потенциалы .

Мировые линии в общей теории относительности

Использование мировых линий в общей теории относительности в основном такое же, как и в специальной теории относительности, с той разницей, что пространство-время можно искривить. Динамика метрики определяется уравнениями Эйнштейна и зависит от распределения массы и энергии в пространстве-времени. Метрика определяет светоподобные (нулевые), пространственноподобные и времениподобные кривые. Кроме того, в общей теории относительности мировые линии — это времениподобные кривые в пространстве-времени, располагающиеся в световом конусе. Световой конус не обязательно наклонен под углом 45 градусов к оси времени. Однако это артефакт выбранной системы координат и отражает координатную свободу (инвариантность диффеоморфизма) общей теории относительности. Любая времениподобная кривая допускает сопутствующего наблюдателя, чья «временная ось» соответствует этой кривой, и, поскольку ни один наблюдатель не имеет преимущества, мы всегда можем найти локальную систему координат, в которой световые конусы наклонены под углом 45 градусов к оси времени. См. также, например, координаты Эддингтона-Финкельштейна.

Мировые линии свободно падающих частиц или объектов (например, планет вокруг Солнца или космонавта в космосе) называются геодезическими.

Мировые линии в квантовой теории поля

Квантовая теория поля, структура, в которой описывается вся современная физика элементарных частиц, обычно описывается как теория квантованных полей. Однако, хотя она и не получила широкого признания, со времен Фейнмана известно, что многие квантовые теории поля могут быть эквивалентно описаны в терминах мировых линий. Формулировка квантовой теории поля через мировые линии (см англоязычный вариант статьи) оказалась особенно полезной для различных вычислений в калибровочных теориях и для описания нелинейных эффектов электромагнитных полей.

См. также

• Конкретные типы мировых линий
  • Геодезические
  • Замкнутые времениподобные кривые
  • Причинная структура, кривые, которые представляют множество различных типов мировых линий
  • Изотропная линия
• Диаграмма Фейнмана
• География времени

Ссылки

• Minkowski, Hermann (1909), "Raum und Zeit" , Physikalische Zeitschrift, 10: 75—88
  • Различные переводы на английский язык в Википедии: Пространство и время
• Людвик Зильберштейн (1914) Теория относительности, стр. 130, Macmillan and Company .
• Мировые линии статья на h2g2 .
• Подробная статья о мировых линиях и специальной теории относительности

Литература

• Ландау Л. Д., Лифшиц Е. М. § 2. Интервал. § 3. Собственное время. § 7. Четырехмерная скорость // Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7..