Пространственно-временная диаграмма

Пространственно-временная диаграмма, также известная как Диаграмма Минковского, была разработана в 1908 г. Германом Минковским и дает иллюстрацию свойств пространства и времени в специальной теории относительности. Она позволяет без математических уравнений качественно понимать такие явления, как замедление времени и Лоренцево сокращение.
Диаграммы Минковского представляют собой двумерный график, изображающий события, происходящие во вселенной, состоящей из одного пространственного измерения и одного временного измерения. В отличие от обычных графиков «время-расстояние», расстояние отображается на горизонтальной оси, а время — на вертикальной оси. Кроме того, единицы измерения осей выбираются таким образом, что мировая линия объекта, движущегося со скоростью света, изображается под углом 45° к осям диаграммы.
Таким образом, каждый объект, такой как наблюдатель или транспортное средство, отображается определенной линией на диаграмме, которая называется его мировой линией. Кроме того, каждая точка диаграммы представляет собой определенную позицию в пространстве и времени и называется событием, независимо от того, что там происходит.
Основы[править | править код]
Термин «диаграмма Минковского» используется как в общем, так и в частном смысле. В общем случае диаграмма Минковского представляет собой двумерное графическое изображение части пространства Минковского, обычно с ограничением до одного пространственного измерения. Единицы измерения на этих диаграммах взяты так, что световой конус события состоит из линий с угловым коэффициентом плюс или минус единица[1]. Горизонтальные линии соответствуют обычному понятию одновременных событий для стационарного наблюдателя в начале координат.
Отдельная диаграмма Минковского иллюстрирует результат преобразований Лоренца. Преобразования Лоренца связывают две инерциальные системы отсчета, где неподвижный наблюдатель покоящийся в (0, 0) изменяет скорость вдоль оси x. Новая ось времени наблюдателя образует угол α с предыдущей временной осью с α < . В новой системе отсчета одновременные события лежат параллельно линии, наклоненной на α к предыдущей линии одновременности. Это — новая ось x. И исходное множество осей, и новый набор осей обладают свойством, что они ортогональны относительно внутреннего (скалярного) произведения в пространстве Минковского или релятивистского произведения в точке.
Какова бы ни была величина α, линия t = x образует универсальную[2] биссекцию.
Единицы измерения пространственных и временной оси могут быть выбраны, например, так:
- Единицы длины 30 сантиметров и наносекунды
- Астрономическая единица и интервалы в 8 минут и 20 секунд (500 секунд)
- световые года и года
- Световые секунды и секунды
Таким образом, световые пути представлены линиями, параллельными биссектрисе угла между осями.
Пространственно-временные диаграммы в физике Ньютона[править | править код]

Черные оси, обозначенные x и ct на прилагающейся диаграмме, представляют собой систему координат покоящегося наблюдателя, который находится в x = 0. Мировая линия наблюдателя совпадает с осью времени ct. Каждая параллельная этой оси линия будет соответствовать неподвижному объекту, но в другом положении. Синяя линия описывает объект, движущийся с постоянной скоростью v вправо, например, движущийся наблюдатель.
Синяя линия с надписью ct' может быть интерпретирована как ось времени для второго наблюдателя. Вместе с осью пути (обозначается x и идентична для обоих наблюдателей) представляет собой их систему координат. Оба наблюдателя согласны с расположением начал координат их координатных систем. Оси движущегося наблюдателя не являются перпендикулярными друг к другу, а масштаб на его временной оси растянут. Чтобы определить координаты определенного события, должны быть построены две линии, каждая из которых параллельна одной из двух осей, проходящих через событие. Их пересечения с осями дают координаты события.
Определение положения и времени события A на диаграмме, как и ожидалось, приводит к одинаковому времени для обоих наблюдателей. Разные значения получаются для позиции, потому что движущийся наблюдатель приблизился к позиции события A, так как t = 0. Как правило, все события на линии, параллельной оси пути (оси x), происходят одновременно для обоих наблюдателей. Существует только одно глобальное время t = t′, моделирующее существование одной общей оси положения. С другой стороны, из-за двух разных осей времени наблюдатели обычно измеряют разные координаты пути для одного и того же события. Это графическое преобразование из x и t в x' и t' , и наоборот, математически описывается так называемыми преобразованиями Галилея.
Пространственно-временные диаграммы в специальной теории относительности[править | править код]

Альберт Эйнштейн (1905) обнаружил, что ньютоновское описание неверно[3]. Герман Минковский в 1908 году предоставил свою графическую интерпретацию[4]. Пространство и время имеют свойства, которые приводят к различным правилам для преобразования координат в случае движущихся наблюдателей. В частности, события, которые происходят одновременно с точки зрения одного наблюдателя, происходят в разное время для другого.
На диаграмме Минковского эта относительность одновременности соответствует введению отдельной оси пути для движущегося наблюдателя. Следуя описанному выше правилу, каждый наблюдатель интерпретирует все события на линии, параллельной оси его пути, одновременно. Последовательность событий с точки зрения наблюдателя может быть проиллюстрирована графически, сдвигая эту линию на диаграмме снизу вверх.
Если осям времени назначить ct вместо t, то угол α между обеими осями пути x и x' будет идентичен углу между осями времени ct и ct' . Это следует из второго постулата специальной теории относительности, в котором говорится, что скорость света одинакова для всех наблюдателей, независимо от их относительного движения (см. ниже). Угол α задается формулой[5]
- .

Соответствующее преобразование из x и t в x' и t' и наоборот, математически описывается преобразованиями Лоренца. Независимо от того, какие пространственные и временные оси возникают при таком преобразовании, на диаграмме Минковского они соответствуют сопряженным диаметрам пары гипербол. Масштабы по осям даны следующим образом: если U — единичная длина по осям ct и x соответственно, то длина единицы по осям ct' и x' равна:[6]
Ось ct — мировая линия часов, покоящихся в S, U представляет продолжительность между двумя событиями, происходящими на этой мировой линии, также называемые собственным временем между этими событиями. Длина U на оси x представляет собственную длину стержня, покоящегося в S. Та же интерпретация также может быть применена к расстоянию U' на ct' - и x' -осях для часов и стержней, покоящихся в S' .
Диаграммы Лоеделя[править | править код]



В то время как пространственная и временная оси покоящейся системы отсчёта находятся под прямым углом, в движущейся системе отсчета оси образуют острый угол. Поскольку системы отсчета должны быть эквивалентными, создается впечатление, что такая асимметрия нарушает эквивалентность. Тем не менее было показано, что существует промежуточная система отсчета «между» покоящейся и движущейся, в которой видно эту симметрию («промежуточная система отсчета»)[7]. В этой системе отсчета две исходные системы отсчета движутся в противоположных направлениях с равной скоростью. Использование таких координат делает единицы длины и времени для обеих осей одинаковыми. Если β = v/c и γ = 1/√1 − β2 заданы между S и S', то эти выражения связаны со значениями в промежуточной системе S0 следующим образом:[7][8]
Например, если между S и S' β = 0.5, то в силу (2) они перемещаются в промежуточной системе S0 примерно с ±0.268c в разных направлениях. С другой стороны, если β0 = 0.5 в S0, то в силу (1) относительная скорость между S и S' в своих собственных системах отсчета 0.8c. Построение осей S и S' выполняется в соответствии с обычным методом с использованием tan α = β0 по отношению к ортогональным осям промежуточной системы отсчета (рис.1).
Однако, оказывается, что при построении такой симметричной диаграммы можно получить отношения диаграмм, даже вообще не используя промежуточную систему отсчета и β0. Вместо этого между S и S' может быть непосредственно использована относительная скорость β = v/c в следующем выражении, обеспечивающем тот же результат:[9] Если φ - угол между осями ct′ и ct (или между x и x′), и θ между осями x′ и ct′, то:[9][10][11][12]
Из рис.2 очевидны два способа построения: (а) ось x направлена перпендикулярно оси ct' , x' и ct-оси добавляются под углом φ; (b) ось x' рисуется под углом θ относительно оси ct' , x-ось добавляется перпендикулярно оси ct' , ось ct - перпендикулярно х' -оси.
Компоненты вектора могут быть наглядно продемонстрированы следующими диаграммами (рис.3): параллельные проекции (x, t; x′ ,t′) вектора R - его контравариантные компоненты, (ξ, τ; ξ′, τ′) - его ковариантные компоненты[10][11].
Замедление времени[править | править код]
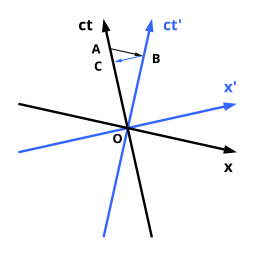
Релятивистское замедление времени означает, что часы (показывающие собственное время), которые перемещаются относительно наблюдателя, идут замедленно. Фактически, само время в системе отсчета движущихся часов наблюдается замедленным. Это можно сразу же увидеть из соседней диаграммы Лоеделя, потому что единицы длины в двух системах осей идентичны. Таким образом, чтобы сравнить показания между двумя системами, мы можем просто сравнить длины, как они видны на странице: нам не нужно учитывать тот факт, что единицы длины на каждой оси искажаются фактором
который мы должны были бы учитывать на соответствующей диаграмме Минковского.
Предполагается, что наблюдатель, чья система отсчета задана черными осями, перемещается от начала O к A. Движущиеся часы имеют систему отсчета, заданную синими осями, и перемещаются от O до B. Для черного наблюдателя все события, происходящие одновременно с событием в точке А, расположены на линии, параллельной его пространственной оси. Эта линия проходит через A и B, поэтому A и B являются одновременными для системы отсчета наблюдателя с черными осями. Однако часы, движущиеся относительно черного наблюдателя, отмечают время по синей оси времени. Это представлено расстоянием от O до B. Следовательно, наблюдатель в точке A с черными осями считает показания своих часов соответствующих расстоянию от O до A, в то время как для движущихся относительно себя часов - расстоянию от O до B. Из-за того, что расстояние от O до B меньше, чем расстояние от O до A, он заключает, что время, прошедшее на часах, движущихся относительно него, меньше, чем время, прошедшее на его собственных часах.
Второй наблюдатель, двигаясь вместе с часами от O до B, будет утверждать, что часы первого достигли только момента C, и поэтому часы первого работают медленнее. Причиной этих кажущихся парадоксальными высказываний является разное определение одновременности событий, происходящих в разных местах. Из-за принципа относительности вопрос о том, кто прав, не имеет ответа и не имеет смысла.
Лоренцево сокращение[править | править код]
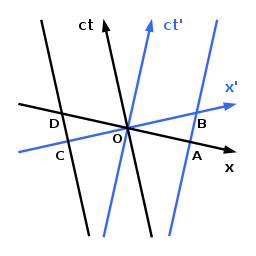
Релятивистское сокращение длины означает, что длина объекта, движущегося относительно наблюдателя, уменьшается, и, даже само пространство сжимается. Предполагается, что наблюдатель также движется вдоль оси ct, и что мировые линии крайних точек движущегося относительно него объекта перемещаются вдоль оси ct' и параллельно линии, проходящей через точки A и B. Для этого наблюдателя крайние точки объекта в t=0 - это O и A. Для второго наблюдателя, движущегося вместе с объектом, так что для него объект находится в состоянии покоя, он имеет собственную длину OB при t' =0. Так как OA<OB объект оказывается уменьшенным для первого наблюдателя.
Второй наблюдатель будет утверждать, что первый наблюдатель взял конечные точки объекта в O и A в разное время, что привело к неправильному результату. Если второй наблюдатель найдет длину другого объекта с конечными точками, движущимися вдоль оси ct и параллельной линией, проходящей через C и D, он придет к такому же выводу, что объект сжат с OD до OC. Каждый наблюдатель оценивает объекты, двигающиеся с другим наблюдателем, уменьшенными. Эта кажущаяся парадоксальной ситуация является следствием относительности одновременности, о чем свидетельствует анализ при помощи диаграммы Минковского.
При всех этих соображениях предполагалось, что оба наблюдателя учитывают скорость света и расстояния до всех событий, которые они видят, для определения фактических моментов, в которых происходят события с их точек зрения.
Постоянство скорости света[править | править код]

Другим постулатом специальной теории относительности является постоянство скорости света. В нем говорится, что любой наблюдатель в инерциальной системе отсчета, измеряющий относительно себя скорость света в вакууме, получает одно и то же значение независимо от его собственного движения и движения источника света. Это утверждение представляется парадоксальным, но оно непосредственно следует из полученного для него дифференциального уравнения, и согласуется с диаграммой Минковского. Это объясняет также результат опыта Майкельсона-Морли, который считался загадкой до того, как была открыта теория относительности, когда фотоны считались волнами в необнаружимой среде.
Для мировых линий фотонов, проходящих через начало координат в разных направлениях, выполняются условия x = ct и x = −ct. Это означает, что любая позиция на такой мировой линии соответствует одинаковым значениям координат по осям x и ct. Из правила для получения координат в системе координат с наклонными осями следует, что эти две мировые линии являются биссектрисами углов, образованного осями x и ct. Диаграмма Минковского показывает, что они также являются биссектрисами углов, образованных осями x' и ct' . Это означает, что оба наблюдателя измеряют одну и ту же скорость c для обоих фотонов.
Остальные системы координат, соответствующие наблюдателям с произвольными скоростями, можно также добавить на эту диаграмму Минковского. Для всех этих систем мировые линии фотонов представляют собой биссектрисы углов, образованных осями координат. Чем ближе скорость наблюдателя к скорости света, тем больше оси приближаются к соответствующим биссектрисам углов. Ось пути всегда более пологая, а ось времени - более крутая, чем мировые линии фотонов. Масштабы по обеим осям всегда одинаковы, но обычно отличаются от других систем координат.
Скорость света и принцип причинности[править | править код]

Прямые линии, проходящие через начало координат и которые круче мировых линий фотонов, соответствуют телам, двигающимися медленнее скорости света. Это верно с точки зрения любого наблюдателя, поскольку мировые линии фотонов являются биссектрисами углов в любой инерциальной системе отсчета. Поэтому любая точка, находящаяся выше начала координат и между мировыми линиями обоих фотонов, может быть достигнута со скоростью, меньшей чем скорость света, и может иметь причинно-следственную связь с началом координат. Эта область является абсолютным будущим, потому что любое событие в этой области происходит позже чем событие в начале координат, независимо от наблюдателя, что хорошо видно на диаграмме Минковского.
Аналогично область, находящаяся ниже начала координат и между мировыми линиями фотонов, является абсолютным прошлым относительно начала координат. Любое событие из этой области может быть причиной события в начале координат.
Связь между любыми такими парами событий называется времениподобной, потому что для всех наблюдателей между ними есть ненулевой положительный промежуток времени. Прямая линия, соединяющая два таких события, всегда может являться осью времени какого-либо наблюдателя, для которого эти события происходят в одном и том же месте пространства. Два события, которые могут быть связаны только линией, соответствующей скорости света, называются светоподобными.
На диаграмму Минковского можно добавить еще одну размерность пространства, приводящую к трехмерному представлению. В этом случае области будущего и прошлого становятся конусами с вершинами, касающимися друг друга в начале координат. Их называют световыми конусами.
Скорость света как предел[править | править код]

Аналогично примеру выше, все прямые, проходящие через начало координат и более горизонтально, чем мировые линии фотонов, будут соответствовать объектам или сигналам, движущимся быстрее скорости света, независимо от скорости наблюдателя. Следовательно, никакое событие вне световых конусов не может быть достигнуто из начала координат ни световым сигналом, ни каким-либо объектом или сигналом, движущимся с меньшей скоростью, чем скорость света. Такие пары событий называются пространственноподобными, поскольку для всех наблюдателей они имеют конечное ненулевое пространственное расстояние. Прямая линия, соединяющая такие события, всегда является пространственной координатной осью возможного наблюдателя, для которого эти события происходят одновременно. Небольшим изменением скорости этой системы координат в обоих направлениях всегда можно найти две инерциальные системы отсчета, наблюдатели которых считают разным хронологический порядок этих событий.
Таким образом, если объект, двигается быстрее света, например, от O до A как показано на диаграмме рядом, то это будет означать, что для любого наблюдателя, наблюдающего за перемещением объекта от O до A, можно найти еще одного наблюдателя (движущегося со скоростью меньше, чем скорость света с по отношению к первому), для которого объект перемещается от А к О. Вопрос о том, какой наблюдатель прав, не имеет однозначного ответа и поэтому не имеет никакого физического смысла. Любой объект или сигнал, двигающийся таким образом, нарушат принцип причинности.
Кроме того, наличие возможности отправки сигналов быстрее скорости света, позволят передавать информацию в собственное прошлое источника. На диаграмме наблюдатель в O в системе x-ct посылает сообщение, движущееся быстрее света, в A. В точке A оно принимается другим наблюдателем в системе x' -ct' (то есть имеющего другую скорость), который отправляет ее назад, также быстрее скорости света, в B. Но B находится в прошлом по отношению к O. Абсурдность ситуации заключается в том, что оба наблюдателя впоследствии подтверждают, что они вообще не получали сообщения, а все сообщения не принимались, а отправлялись от каждого к другому наблюдателю, как это видно на диаграмме Минковского. Кроме того, если бы можно было ускорить наблюдателя до скорости света, то их пространственная и временная оси совпадали бы биссектрисой их угла. Система координат рухнула бы из-за того, что замедление времени достигает такого значения, что ход времени просто останавливается.
Эти соображения показывают, что предел скорости света является следствием свойств пространства-времени, а не свойств объектов, как, например, технологически - несовершенство космических кораблей. Таким образом, запрет на движение быстрее скорости света в пространстве Минковского не имеет ничего общего с электромагнитными волнами или светом, а возникает из-за структуры пространства-времени.
Пространственно-временные диаграммы ускоряющегося наблюдателя в специальной теории относительности[править | править код]

Мгновенно сопутствующие инерциальные системы отсчета вдоль мировой линии быстро ускоряющегося наблюдателя (в центре). Вертикальное направление указывает время, горизонтальное - расстояние, пунктирная линия - это пространственно-временная траектория («мировая линия») наблюдателя. Маленькие точки - это конкретные события в пространстве-времени. Если вообразить эти события как вспышку света, события, которые проходят две диагональные линии в нижней половине изображения (световой конус прошлого наблюдателя, находящегося в начале координат), являются событиями, видимыми наблюдателю. Наклон мировой линии (отклонение от вертикали) дает относительную скорость наблюдателя. Обратите внимание на то, как мгновенно сопутствующая инерциальная система отсчета изменяется при ускорениях наблюдателя.
См также[править | править код]
Примечания[править | править код]
- ↑ Mermin (1968) Chapter 17
- ↑ См Владимир Карапетов
- ↑ Einstein, Albert. Zur Elektrodynamik bewegter Körper (неопр.) // Annalen der Physik. — 1905. — Т. 322, № 10. — С. 891—921. — doi:10.1002/andp.19053221004. — . Архивировано 24 сентября 2015 года.. См также: English translation Архивная копия от 25 ноября 2005 на Wayback Machine.
- ↑ Minkowski, Hermann. Raum und Zeit (нем.) // Physikalische Zeitschrift : magazin. — 1909. — Bd. 10. — S. 75—88.
- Различные переводы на Wikisource: Space and Time
- ↑ Demtröder, Wolfgang. Mechanics and Thermodynamics (англ.). — illustrated. — Springer, 2016. — P. 92—93. — ISBN 978-3-319-27877-3. Extract of page 93 Архивная копия от 11 августа 2020 на Wayback Machine
- ↑ Freund, Jürgen. Special Relativity for Beginners: A Textbook for Undergraduates (англ.). — World Scientific, 2008. — P. 49. — ISBN 981277159X.
- ↑ 1 2 Mirimanoff, Dmitry. La transformation de Lorentz-Einstein et le temps universel de M. Ed. Guillaume (фр.) // Archives des sciences physiques et naturelles (supplement) : magazine. — 1921. — Vol. 3. — P. 46—48. Архивировано 22 августа 2018 года. (Translation: The Lorentz-Einstein transformation and the universal time of Ed. Guillaume)
- ↑ Shadowitz, Albert. The Electromagnetic Field (англ.). — Reprint of 1975. — Courier Dover Publications, 2012. — P. 460. — ISBN 0486132013. See Google books, p. 460
- ↑ 1 2 Sartori, Leo. Understanding Relativity: A simplified approach to Einstein's theories (англ.). — University of California Press, 1996. — P. 151ff. — ISBN 0-520-20029-2.
- ↑ 1 2 Gruner, Paul; Sauter, Josef. Représentation géométrique élémentaire des formules de la théorie de la relativité (фр.) // Archives des sciences physiques et naturelles : magazine. — 1921. — Vol. 3. — P. 295—296. Архивировано 3 сентября 2018 года. (Translation: Elementary geometric representation of the formulas of the special theory of relativity)
- ↑ 1 2 Gruner, Paul. Eine elementare geometrische Darstellung der Transformationsformeln der speziellen Relativitätstheorie (нем.) // Physikalische Zeitschrift : magazin. — 1921. — Bd. 22. — S. 384—385. (Translation: An elementary geometrical representation of the transformation formulas of the special theory of relativity)
- ↑ Shadowitz, Albert. Special Relativity (англ.). — Reprint of 1968. — Courier Dover Publications, 1988. — P. 20—22. — ISBN 0-486-65743-4.
Источники[править | править код]
- Anthony French (1968) Special Relativity, pages 82 & 83, New York: W W Norton & Company.
- E.N. Glass (1975) "Lorentz boosts and Minkowski diagrams" American Journal of Physics 43:1013,4.
- N. David Mermin (1968) Space and Time in Special Relativity, Chapter 17 Minkowski diagrams: The Geometry of Spacetime, pages 155–99 McGraw-Hill.
- Rindler, Wolfgang. Relativity: Special, General and Cosmological (англ.). — Oxford University Press, 2001. — ISBN 0-19-850836-0.
- W.G.V. Rosser (1964) An Introduction to the Theory of Relativity, page 256, Figure 6.4, London: Butterworths.
- Edwin F. Taylor and John Archibald Wheeler (1963) Spacetime Physics, pages 27 to 38, New York: W. H. Freeman and Company, Second edition (1992).
- Walter, Scott (1999), "The non-Euclidean style of Minkowskian relativity" (PDF), in J. Gray (ed.), The Symbolic Universe: Geometry and Physics, Oxford University Press, pp. 91—127 (see page 10 of e-link)





