Функции Бесселя

Фу́нкции Бе́сселя в математике — семейство функций, являющихся каноническими решениями дифференциального уравнения Бесселя:

$x^{2}{\frac {d^{2}y}{dx^{2}}}+x{\frac {dy}{dx}}+(x^{2}-\alpha ^{2})y=0,$

где $\alpha$ — произвольное вещественное число (в общем случае комплексное), называемое порядком.

График функций Бесселя первого рода

Наиболее часто используемые функции Бесселя — функции целых порядков.

Хотя $\alpha$ и $(-\alpha )$ порождают одинаковые уравнения, обычно договариваются о том, чтобы им соответствовали разные функции (это делается, например, для того, чтобы функция Бесселя была гладкой по $\alpha$).

Функции Бесселя впервые были определены швейцарским математиком Даниилом Бернулли, а названы в честь Фридриха Бесселя.

Применения

Уравнение Бесселя возникает во время нахождения решений уравнения Лапласа и уравнения Гельмгольца в цилиндрических и сферических координатах. Поэтому функции Бесселя применяются при решении многих задач о распространении волн, статических потенциалах и т. п., например:

• электромагнитные волны в цилиндрическом волноводе;
• теплопроводность в цилиндрических объектах;
• формы колебания тонкой круглой мембраны;
• распределение интенсивности света, дифрагированного на круглом отверстии;
• скорость частиц в цилиндре, заполненном жидкостью и вращающемся вокруг своей оси;
• волновые функции в сферически симметричном потенциальном ящике.

Функции Бесселя применяются и в решении других задач, например, при обработке сигналов.

Функция Бесселя является обобщением функции синуса. Ее можно трактовать как колебание струны с переменной толщиной, переменным натяжением (или одновременно обоими условиями); колебаниями в среде с переменными свойствами; колебаниями дисковой мембраны и т. д.

Определения

Поскольку приведённое уравнение является линейным дифференциальным уравнением второго порядка, у него должно быть два линейно независимых решения. Однако в зависимости от обстоятельств выбираются разные определения этих решений. Ниже приведены некоторые из них.

Функции Бесселя первого рода

Функциями Бесселя первого рода, обозначаемыми $J_{\alpha }(x)$, являются решения, конечные в точке $x=0$ при целых или неотрицательных $\alpha$. Выбор конкретной функции и её нормализации определяются её свойствами. Можно определить эти функции с помощью разложения в ряд Тейлора около нуля (или в более общий степенной ряд при нецелых $\alpha$):

$J_{\alpha }(x)=\sum _{m=0}^{\infty }{\frac {(-1)^{m}}{m!\,\Gamma (m+\alpha +1)}}{\left({\frac {x}{2}}\right)}^{2m+\alpha }.$

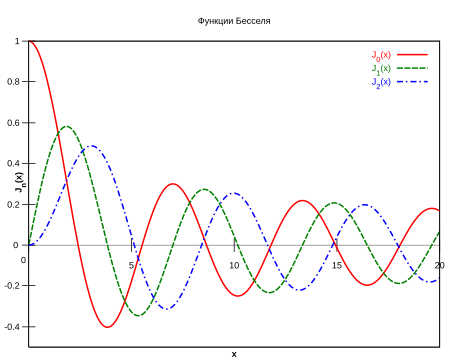
Здесь $\Gamma (z)$ — это гамма-функция Эйлера, обобщение факториала на нецелые значения. График функции Бесселя похож на синусоиду, колебания которой затухают пропорционально ${\frac {1}{\sqrt {x}}}$, хотя на самом деле нули функции расположены не периодично (однако расстояние между двумя последовательными нулями стремится к $\pi$ при $x\to \infty$).

Ниже приведены графики $J_{\alpha }(x)$ для $\alpha =0,1,2$:

График функции Бесселя первого рода J

Если $\alpha$ не является целым числом, функции $J_{\alpha }(x)$ и $J_{-\alpha }(x)$ линейно независимы и, следовательно, являются решениями уравнения. Но если $\alpha$ целое, то верно следующее соотношение:

$J_{-\alpha }(x)=(-1)^{\alpha }J_{\alpha }(x).$

Оно означает, что в этом случае функции линейно зависимы. Тогда вторым решением уравнения станет функция Бесселя второго рода (см. ниже).

Интегралы Бесселя

Можно дать другое определение функции Бесселя для целых значений $\alpha$, используя интегральное представление:

$J_{\alpha }(x)={\frac {1}{\pi }}\int \limits _{0}^{\pi }\!\cos(\alpha \tau -x\sin \tau )\,d\tau .$

Этот подход использовал Бессель, изучив с его помощью некоторые свойства функций. Возможно и другое интегральное представление:

$J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(\alpha \tau -x\sin \tau )}\,d\tau .$

Для нахождения интегрального представления функции Бесселя в случае нецелых $\alpha$ необходимо учесть, что имеется разрез вдоль оси абсцисс. Это вызвано тем, что подынтегральное выражение более не является $2\pi$-периодическим. Таким образом, контур интегрирования разбивается на 3 участка: луч от $-\infty$ до $1$, где ${\textstyle \varphi =-\pi }$, окружность единичного радиуса и луч от $1$ до $+\infty$ при ${\textstyle \varphi =\pi }$. Проделав несложные математические преобразования, можно получить следующее интегральное представление:

$J_{\alpha }(x)={\frac {1}{2\pi }}\int \limits _{-\pi }^{\pi }\!e^{i(x\sin(\varphi )-\alpha \varphi )}d\varphi -{\frac {\sin(\alpha \pi )}{\pi }}\int \limits _{1}^{\infty }{\frac {e^{-{\frac {1}{2}}x(r-{\frac {1}{r}})}}{{}r^{\alpha +1}}}dr.$

Нетрудно убедиться, что при целых $\alpha$ это выражение переходит в предыдущую формулу.

Функции Неймана

Функции Неймана — решения $Y_{\alpha }(x)$ уравнения Бесселя, бесконечные в точке $x=0$.

Эта функция связана с $J_{\alpha }(x)$ следующим соотношением:

$Y_{\alpha }(x)={\frac {J_{\alpha }(x)\cos(\alpha \pi )-J_{-\alpha }(x)}{\sin(\alpha \pi )}},$

где в случае целого $\alpha$ берётся предел по $\alpha$, вычисляемый, например, с помощью правила Лопиталя.

Функции Неймана также называются функциями Бесселя второго рода. Линейная комбинация функций Бесселя первого и второго родов являет собой полное решение уравнения Бесселя:

$y(x)=C_{1}J_{\alpha }(x)+C_{2}Y_{\alpha }(x).$

Ниже приведён график $Y_{\alpha }(x)$ для $\alpha =0,1,2$:

График функции Бесселя второго рода N

В ряде книг функции Неймана обозначаются $N_{\alpha }(x)$.

Сферические функции Бесселя

Сферические функции Бесселя первого рода, j_n(x), для n = 0, 1, 2

Сферические функции Бесселя второго рода, y_n(x), для n = 0, 1, 2

При решении уравнения Гельмгольца в сферических координатах методом разделения переменных уравнение на радиальную часть имеет вид

$x^{2}{\frac {d^{2}y}{dx^{2}}}+2x{\frac {dy}{dx}}+\left(x^{2}-n(n+1)\right)y=0.$

Два линейно-независимых решения называются сферическими функциями Бесселя j_n и y_n, и связаны с обычными функциями Бесселя J_n и Неймана Y_n с помощью

${\begin{aligned}j_{n}(x)&={\sqrt {\frac {\pi }{2x}}}J_{n+{\frac {1}{2}}}(x),\\y_{n}(x)&={\sqrt {\frac {\pi }{2x}}}Y_{n+{\frac {1}{2}}}(x)=(-1)^{n+1}{\sqrt {\frac {\pi }{2x}}}J_{-n-{\frac {1}{2}}}(x).\end{aligned}}$

y_n также обозначается n_n или η_n; некоторые авторы называют эти функции сферическими функциями Неймана.

Сферические функции Бесселя также могут быть записаны как (формула Релея)

${\begin{aligned}j_{n}(x)&=(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\sin x}{x}},\\y_{n}(x)&=-(-x)^{n}\left({\frac {1}{x}}{\frac {d}{dx}}\right)^{n}{\frac {\cos x}{x}}.\end{aligned}}$

Несколько первых сферических функций Бесселя:

${\begin{aligned}j_{0}(x)&={\frac {\sin x}{x}},\\j_{1}(x)&={\frac {\sin x}{x^{2}}}-{\frac {\cos x}{x}},\\j_{2}(x)&=\left({\frac {3}{x^{2}}}-1\right){\frac {\sin x}{x}}-{\frac {3\cos x}{x^{2}}},\\j_{3}(x)&=\left({\frac {15}{x^{3}}}-{\frac {6}{x}}\right){\frac {\sin x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\cos x}{x}}\end{aligned}}$

и Неймана:

${\begin{aligned}y_{0}(x)&=-j_{-1}(x)=-{\frac {\cos x}{x}},\\y_{1}(x)&=j_{-2}(x)=-{\frac {\cos x}{x^{2}}}-{\frac {\sin x}{x}},\\y_{2}(x)&=-j_{-3}(x)=\left(-{\frac {3}{x^{2}}}+1\right){\frac {\cos x}{x}}-{\frac {3\sin x}{x^{2}}},\\y_{3}(x)&=j_{-4}(x)=\left(-{\frac {15}{x^{3}}}+{\frac {6}{x}}\right){\frac {\cos x}{x}}-\left({\frac {15}{x^{2}}}-1\right){\frac {\sin x}{x}}.\end{aligned}}$

Производящие функции

Производящие функции сферических функций Бесселя:

${\begin{aligned}{\frac {1}{z}}\cos \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}j_{n-1}(z),\\{\frac {1}{z}}\sin \left({\sqrt {z^{2}-2zt}}\right)&=\sum _{n=0}^{\infty }{\frac {t^{n}}{n!}}y_{n-1}(z).\end{aligned}}$

Дифференциальные соотношения

В следующих формулах f_n может быть заменено на j_n, y_n, h(1)
n, h(2)
n, где h(1)
n и h(2)
n — сферические функции Ханкеля, для n = 0, ±1, ±2, ...:

${\begin{aligned}\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{n+1}f_{n}(z)\right)&=z^{n-m+1}f_{n-m}(z),\\\left({\frac {1}{z}}{\frac {d}{dz}}\right)^{m}\left(z^{-n}f_{n}(z)\right)&=(-1)^{m}z^{-n-m}f_{n+m}(z).\end{aligned}}$

Свойства

Ортогональность

Пусть $\mu _{1},\mu _{2}$ — нули функции Бесселя $J_{\alpha }(x)$. Тогда:

$\int _{0}^{1}{xJ_{\alpha }(\mu _{1}x)J_{\alpha }(\mu _{2}x)dx}=\left\{{\begin{matrix}0&{\mbox{;}}\quad \mu _{1}\neq \mu _{2}\\\\{\frac {1}{2}}(J'_{\alpha }(\mu _{1}))^{2}&{\mbox{;}}\quad \mu _{1}=\mu _{2}\end{matrix}}\right.$.

Асимптотика

Для функций Бесселя первого и второго рода известны асимптотические формулы. При малых аргументах $(0<x\ll {\sqrt {\alpha +1}})$ и неотрицательных $\alpha$ они выглядят так:

$J_{\alpha }(x)\rightarrow {\frac {1}{\Gamma (\alpha +1)}}\left({\frac {x}{2}}\right)^{\alpha },$

$Y_{\alpha }(x)\rightarrow \left\{{\begin{matrix}{\frac {2}{\pi }}\left[\ln(x/2)+\gamma \right]&{\mbox{;}}\quad \alpha =0\\\\-{\frac {\Gamma (\alpha )}{\pi }}\left({\frac {2}{x}}\right)^{\alpha }&{\mbox{;}}\quad \alpha >0\end{matrix}}\right.$,

где $\gamma$ — постоянная Эйлера — Маскерони (0,5772…), а $\Gamma$ — гамма-функция Эйлера. Для больших аргументов ($x\gg |\alpha ^{2}-1/4|$) формулы выглядят так:

$J_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right),$

$Y_{\alpha }(x)\rightarrow {\sqrt {\frac {2}{\pi x}}}\sin \left(x-{\frac {\alpha \pi }{2}}-{\frac {\pi }{4}}\right).$

Использование следующего члена асимптотического разложения позволяет значительно уточнить результат. Для функции Бесселя нулевого порядка он выглядит следующим образом:

$J_{0}\rightarrow {\sqrt {\frac {2}{\pi x}}}\cos(x-{\frac {\pi }{4}})+{\frac {1}{4x{\sqrt {2\pi x}}}}\sin(x-{\frac {\pi }{4}}).$

Гипергеометрический ряд

Функции Бесселя могут быть выражены через гипергеометрическую функцию:

$J_{\alpha }(z)={\frac {(z/2)^{\alpha }}{\Gamma (\alpha +1)}}{}_{0}F_{1}(\alpha +1;-z^{2}/4).$

Таким образом, при целых $\alpha$ функция Бесселя однозначная аналитическая, а при нецелых — многозначная аналитическая.

Производящая функция

Существует представление для функций Бесселя первого рода и целого порядка через коэффициенты ряда Лорана функции определённого вида, а именно

$e^{{\frac {z}{2}}\left(w-{\frac {1}{w}}\right)}=\sum _{n=-\infty }^{+\infty }J_{n}(z)w^{n}.$

Соотношения

Формула Якоби — Ангера и связанные с ней

Получается из выражения для производящей функции при $a=1$, $w=e^{i\phi }$:

$e^{iz\sin \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }J_{2n}(z)\cos(2n\phi )+2i\sum _{n=1}^{\infty }J_{2n-1}(z)\sin(2n-1)\phi .$

При $a=1$, $t=ie^{i\phi }$:

$e^{iz\cos \phi }=J_{0}(z)+2\sum _{n=1}^{\infty }i^{n}J_{n}(z)\cos(n\phi ).$

Рекуррентные соотношения

Для функций Бесселя существует ряд рекуррентных соотношений. Приведём здесь некоторые из них:

$J_{\alpha +1}={\frac {\alpha }{x}}J_{\alpha }-J'_{\alpha }(x);$

$J_{\alpha +1}(x)+J_{\alpha -1}(x)={\frac {2\alpha }{x}}J_{\alpha }(x);$

$J_{\alpha +1}(x)-J_{\alpha -1}(x)=-2J'_{\alpha }(x)$.

Теорема сложения

Для любого целого n и комплексных $z_{1}$, $z_{2}$ выполняется

$J_{n}(z_{1}+z_{2})=\sum _{k=-\infty }^{\infty }J_{k}(z_{1})J_{n-k}(z_{2}).$

Интегральные выражения

Для любых $a$ и $b$ (в том числе комплексных) выполняется

$\int _{0}^{\infty }e^{-at}J_{n}(bt)\mathrm {d} t={\frac {b^{n}}{{\sqrt {a^{2}+b^{2}}}({\sqrt {a^{2}+b^{2}}}+a)^{n}}}.$

Частным случаем последней формулы является выражение

$\int _{0}^{\infty }e^{-at}J_{0}(bt)\mathrm {d} t={\frac {1}{\sqrt {a^{2}+b^{2}}}}.$

См. также

• Цилиндрические функции
• Сферические функции
• Модифицированные функции Бесселя
• Функции Ганкеля
• Луч Бесселя

Литература

• Ватсон Г. . Теория бесселевых функций. — М.: ИЛ, 1949.
• Бейтмен Г., Эрдейи А. . Функции Бесселя, функции параболического цилиндра, ортогональные многочлены // Высшие трансцендентные функции. Т. 2. 2-е изд / Пер. с англ. Н. Я. Виленкина. — М.: Наука, 1974. — 296 с.
• Лаврентьев М. А., Шабат Б. В. . Методы теории функций комплексного переменного. — М.: Наука, 1973. — 736 с.