Бэггинг

Бэггинг (от англ. bootstrap aggregating, бутстрэп-агрегирование) — ансамблевый метаалгоритм, предназначенный для улучшения стабильности и точности алгоритмов машинного обучения, используемых в задачах классификации и регрессии. Алгоритм также уменьшает дисперсию и помогает избежать переобучения. Хотя он обычно применяется к методам машинного обучения на основе деревьев решений, его можно использовать с любым видом метода. Бэггинг является частным видом усреднения модели.

Предложен Лео Брейманом в 1994 году.

Описание техники

Если задан стандартный тренировочный набор $D$ размера $n$, бэггинг образует $m$ новых тренировочных наборов $D_{i}$, каждый размером $n'$, путём выборки из $D$ равномерно и с возвратом. При семплинге с возвратом некоторые наблюдения могут быть повторены в каждой $D_{i}$. Если $n'=n$, то для больших $n$ ожидается, что множество $D_{i}$ имеет долю $1-1/e\approx 0{,}63$ уникальных экземпляров из $D$, остальные будут повторениями. Этот вид семплинга известен как бутстрэп-семплинг. Эти $m$ моделей сглаживаются с помощью вышеупомянутых $m$ бутстрэп-выборок и комбинируются путём усреднения (для регрессии) или голосования (для классификации).

Бэггинг ведёт к «улучшению для нестабильных процедур», в которые входят, например, искусственные нейронные сети, деревья классификации и регрессий и выбор подмножеств в линейной регрессии. В 2011 году найдено применение бэггинга для обработки изображений. С другой стороны, метод может слегка ухудшить эффективность стабильных методов, таких как метод K-ближайших соседей.

Пример: зависимость концентрации озона от температуры

Для иллюстрации основных принципов бэггинга ниже приведён анализ связи между озоном и температурой. Анализ осуществлён на языке программирования R).

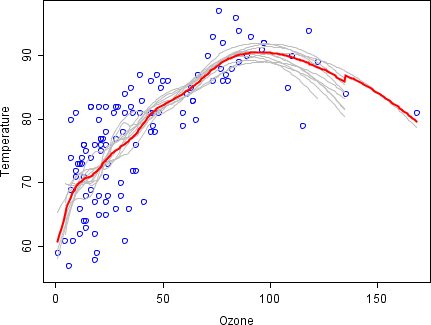
Связь между температурой и озоном в этом наборе данных, очевидно, нелинейна. Чтобы описать эту связь, использовались сглаживатели LOESS (с полосой пропускания 0,5). Вместо построения единого сглаживателя из всего набора данных извлечено 100 выборок бутстрэпов данных. Каждая выборка отличается от исходного набора данных, но они, всё же, совпадают по распределению и дисперсии. Для каждой бутстрэп-выборки применялся сглаживатель LOESS. Затем сделано предсказание по данным на основе этих 100 сглаживаний. Первые 10 сглаживаний показаны серыми линиями на рисунке ниже. Линии, как видно, очень волнисты и страдают переподгонкой данных — результат полосы слишком мал.

Взяв среднее 100 сглаживателей, которые применялись к подмножествам оригинального набора данных, мы получаем сборный предсказатель (красная линия). Ясно, что среднее более устойчиво и не столь подвержено переобучению.

Литература

• Rousseeuw P. J., Leroy A. M. Robust Regression and Outlier Detection. — New York, Chichester, Brisbane, Toronto, Singapure: John Willey & Sons, 1987. — ISBN 0-471-85233-3.
• Javed A. Aslam, Raluca A. Popa, Ronald L. Rivest. On Estimating the Size and Confidence of a Statistical Audit // Proceedings of the Electronic Voting Technology Workshop (EVT '07). — Boston, MA, 2007.
• Sahu A., Runger G., Apley D. Image denoising with a multi-phase kernel principal component approach and an ensemble version // IEEE Applied Imagery Pattern Recognition Workshop. — 2011. — С. 1—7.
• Amit Shinde, Anshuman Sahu, Daniel Apley, George Runger. Preimages for Variation Patterns from Kernel PCA and Bagging // IIE Transactions. — 2014. — Т. 46, вып. 5.
• Leo Breiman. Bagging predictors // Machine Learning. — 1996. — Т. 24, вып. 2. — С. 123–140. — doi:10.1007/BF00058655.
• Breiman L. Bagging Predictors. Technical Report No. 421. — 1994.
• Alfaro E., Gámez M., García N. adabag: An R package for classification with AdaBoost.M1, AdaBoost-SAMME and Bagging. — 2012.