Функция активации

Логистическая функция активации

В искусственных нейронных сетях функция активации нейрона определяет выходной сигнал, который определяется входным сигналом или набором входных сигналов. Стандартная компьютерная микросхема может рассматриваться как цифровая сеть функций активации, которые могут принимать значения «ON» (1) или «OFF» (0) в зависимости от входа. Это похоже на поведение линейного перцептрона в нейронных сетях. Однако только нелинейные функции активации позволяют таким сетям решать нетривиальные задачи с использованием малого числа узлов. В искусственных нейронных сетях эта функция также называется передаточной функцией.

Функции

В биологических нейронных сетях функция активации обычно является абстракцией, представляющей скорость возбуждения потенциала действия в клетке . В наиболее простой форме эта функция является двоичной — то есть нейрон либо возбуждается, либо нет. Функция выглядит как $\phi (v_{i})=U(v_{i})$, где $U$ — ступенчатая функция Хевисайда. В этом случае нужно использовать много нейронов для вычислений за пределами линейного разделения категорий.

Прямая с положительным угловым коэффициентом может быть использована для отражения увеличения скорости возбуждения по мере увеличения входного сигнала. Такая функция имела бы вид $\phi (v_{i})=\mu v_{i}$, где $\mu$ — наклон прямой. Эта функция активации линейна, а потому имеет те же проблемы, что и двоичная функция. Кроме того, сети, построенные с использованием такой модели, имеют нестабильную сходимость, поскольку возбуждение приоритетных входов нейронов стремится к безграничному увеличению, так как эта функция не нормализуема.

Все проблемы, упомянутые выше, можно решить с помощью нормализуемой сигмоидной функции активации. Одна из реалистичных моделей остаётся в нулевом состоянии, пока не придёт входной сигнал, в этот момент скорость возбуждения сначала быстро возрастает, но постепенно достигает асимптоты в 100 % скорости возбуждения. Математически, это выглядит как $\phi (v_{i})=U(v_{i})\mathrm {th} \,(v_{i})$, где гиперболический тангенс можно заменить любой сигмоидой. Такое поведение реально имеет место в биологическом нейроне, поскольку нейроны не могут физически возбуждаться быстрее некоторой определённой скорости. Эта модель, однако, имеет несколько проблем в вычислительных сетях, поскольку функция не дифференцируема, что нужно для вычисления обратной передачи ошибки обучения.

Последняя модель, которая используется в многослойных перцептронах — сигмоидная функция активации в форме гиперболического тангенса. Обычно используются два вида этой функции: $\phi (v_{i})=\mathrm {th} \,(v_{i})$, образ которой нормализован к интервалу [-1, 1], и $\phi (v_{i})=(1+\exp(-v_{i}))^{-1}$, сдвинутая по вертикали для нормализации от 0 до 1. Последняя модель считается более биологически реалистичной, но имеет теоретические и экспериментальные трудности с вычислительными ошибками некоторых типов.

Альтернативные структуры

Специальный класс функций активации, известный как радиальные базисные функции (РБФ) используются в РБФ сетях, которые крайне эффективны в качестве универсальных аппроксиматоров функций. Эти функции активации могут принимать множество форм, но обычно берётся одна из следующих трёх функций:

• Гауссова: $\,\phi (v_{i})=\exp \left(-{\frac {\|v_{i}-c_{i}\|^{2}}{2\sigma ^{2}}}\right)$
• Мультиквадратичная (англ. Multiquadratics): $\,\phi (v_{i})={\sqrt {\|v_{i}-c_{i}\|^{2}+a^{2}}}$
• Обратная мультиквадратичная (англ. Inverse Multiquadratics): $\,\phi (v_{i})=(\|v_{i}-c_{i}\|^{2}+a^{2})^{-1/2}$

где $c_{i}$ является вектором, представляющим центр функции, а $a$ и $\sigma$ являются параметрами, влияющими на расходимость радиуса.

Методы опорных векторов (SVM) могут эффективно использовать класс функций активации, который включает как сигмоиды, так и РБФ. В этом случае вход преобразуется для отражения гиперплоскости границы решений основываясь на нескольких обучающих входных данных, называемых опорными векторами $x$. О функции активации для закрытого уровня этих машин говорят как о ядре скалярного произведения (англ. inner product kernel), $K(v_{i},x)=\phi (v_{i})$. Опорные вектора представляются как центры в РБФ с ядром, равным функции активации, но они принимают единственный вид в перцептроне

$\,\phi (v_{i})=\mathrm {th} \,\left(\beta _{1}+\beta _{0}\sum _{j}v_{i,j}x_{j}\right)$,

где для сходимости $\beta _{0}$ и $\beta _{1}$ должны удовлетворять некоторым условиям. Эти машины могут принимать полиномиальные функции активации любого порядка

$\,\phi (v_{i})=\left(1+\sum _{j}v_{i,j}x_{j}\right)^{p}$.

Функции активации бывают следующих типов:

• Тождественная функция
• Двоичная ступенчатая функция
• Биполярная ступенчатая функция
• Cигмоидная функция
  • Двоичная cигмоидальная функция
  • Биполярная сигмоидная функция
• Функция подъёма

Сравнение функций активации

Некоторые желательные свойства функций активации:

• Нелинейность – Если функция активации нелинейна, можно доказать, что двухуровневая нейронная сеть будет универсальным аппроксиматором функции . Тождественная функция активации не удовлетворяет этому свойству. Если несколько уровней используют тождественную функцию активации, вся сеть эквивалентна одноуровневой модели.
• Непрерывная дифференцируемость – Это свойство желательно (RELU не является непрерывно дифференцируемой и имеет некоторые проблемы с оптимизацией, основанной на градиентном спуске, но остаётся допустимой возможностью) для обеспечения методов оптимизации на основе градиентного спуска. Двоичная ступенчатая функция активации не дифференцируема в точке 0 и её производная равна 0 во всех других точках, так что методы градиентного спуска не дают никакого успеха для неё.
• Область значений – Если множество значений функции активации ограничено, методы обучения на основе градиента более стабильны, поскольку представления эталонов существенно влияют лишь на ограниченный набор весов связей. Если область значений бесконечна, обучение, как правило, более эффективно, поскольку представления эталонов существенно влияют на большинство весов. В последнем случае обычно необходим меньший темп обучения.
• Монотонность – Если функция активации монотонна, поверхность ошибок, ассоциированная с одноуровневой моделью, гарантированно будет выпуклой .
• Гладкие функции с монотонной производной – Показано, что в некоторых случаях они обеспечивают более высокую степень общности.
• Аппроксимирует тождественную функцию около начала координат – Если функции активации имеют это свойство, нейронная сеть будет обучаться эффективно, если её веса инициализированы малыми случайными значениями. Если функция активации не аппроксимирует тождество около начала координат, нужно быть осторожным при инициализации весов. В таблице ниже функции активации, у которых $f(0)=0$, $f'(0)=1$ и $f'$ непрерывна в точке 0, помечены как имеющие это свойство.

Следующая таблица сравнивает свойства некоторых функций активации, которые являются функциями одной свёртки x от предыдущего уровня или уровней:

Название	График	Уравнение	Производная (по x)	Область значений	Порядок гладкости	Монотонная	Монотонная производная	Аппроксимирует тождественную функцию около начала координат
Тождественная		$f(x)=x$	$f'(x)=1$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да
Единичная ступенька		$f(x)={\begin{cases}0&x<0\\1&x\geqslant 0\end{cases}}$	$f'(x)={\begin{cases}0&x\neq 0\\?&x=0\end{cases}}$	$\{0,1\}$	$C^{-1}$	Да	Нет	Нет
Логистическая (сигмоида или Гладкая ступенька)		$f(x)=\sigma (x)={\frac {1}{1+e^{-x}}}$	$f'(x)=f(x)(1-f(x))$	$(0,1)$	$C^{\infty }$	Да	Нет	Нет
th		$f(x)=\mathrm {th} \,(x)={\frac {(e^{x}-e^{-x})}{(e^{x}+e^{-x})}}$	$f'(x)=1-f(x)^{2}$	$(-1,1)$	$C^{\infty }$	Да	Нет	Да
arctg		$f(x)=\mathrm {tg} \,^{-1}(x)$	$f'(x)={\frac {1}{x^{2}+1}}$	$\left(-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$	$C^{\infty }$	Да	Нет	Да
Softsign		$f(x)={\frac {x}{1+|x|}}$	$f'(x)={\frac {1}{(1+|x|)^{2}}}$	$(-1,1)$	$C^{1}$	Да	Нет	Да
Обратный квадратный корень (англ. Inverse square root unit, ISRU)		$f(x)={\frac {x}{\sqrt {1+\alpha x^{2}}}}$	$f'(x)=\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}$	$\left(-{\frac {1}{\sqrt {\alpha }}},{\frac {1}{\sqrt {\alpha }}}\right)$	$C^{\infty }$	Да	Нет	Да
Линейный выпрямитель (или Полулинейный элемент) (англ. Rectified linear unit, ReLU)		$f(x)={\begin{cases}0&x<0\\x&x\geqslant 0\end{cases}}$	$f'(x)={\begin{cases}0&x<0\\1&x\geqslant 0\end{cases}}$	$[0,\infty )$	$C^{0}$	Да	Да	Нет
Линейный выпрямитель с «утечкой» (англ. Leaky rectified linear unit, Leaky ReLU)		$f(x)={\begin{cases}0,01x&x<0\\x&x\geqslant 0\end{cases}}$	$f'(x)={\begin{cases}0,01&x<0\\1&x\geqslant 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да	Да	Нет
Параметрический линейный выпрямитель (англ. Parameteric rectified linear unit, PReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&x<0\\x&x\geqslant 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &x<0\\1&x\geqslant 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да, когда $\alpha \geqslant 0$	Да	Да, когда $\alpha =1$
Рандомизированный линейный выпрямитель с «утечкой» (англ. Randomized leaky rectified linear unit, RReLU)		$f(\alpha ,x)={\begin{cases}\alpha x&x<0\\x&x\geqslant 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}\alpha &x<0\\1&x\geqslant 0\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Да	Да	Нет
Экспоненциальная линейная функция (англ. Exponential linear unit, ELU)		$f(\alpha ,x)={\begin{cases}\alpha (e^{x}-1)&x<0\\x&x\geqslant 0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}f(\alpha ,x)+\alpha &x<0\\1&x\geqslant 0\end{cases}}$	$(-\alpha ,\infty )$	${\begin{cases}C_{1}&\alpha =1\\C_{0}&\alpha \neq 1\end{cases}}$	Да, когда $\alpha \geqslant 0$	Да, когда $0\leqslant \alpha \leqslant 1$	Да, когда $\alpha =1$
Масштабированная экспоненциальная линейная функция (англ. Scaled exponential linear unit, SELU)		$f(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x}-1)&x<0\\x&x\geqslant 0\end{cases}}$ с $\lambda =1,0507$ и $\alpha =1,67326$	$f'(\alpha ,x)=\lambda {\begin{cases}\alpha (e^{x})&x<0\\1&x\geqslant 0\end{cases}}$	$(-\lambda \alpha ,\infty )$	$C^{0}$	Да	Нет	Нет
Линейный S-выпрямитель (англ. S-shaped rectified linear activation unit, SReLU)		$f_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}t_{l}+a_{l}(x-t_{l})&x\leqslant t_{l}\\x&t_{l}<x<t_{r}\\t_{r}+a_{r}(x-t_{r})&x\geqslant t_{r}\end{cases}}$ $t_{l},a_{l},t_{r},a_{r}$ являются параметрами.	$f'_{t_{l},a_{l},t_{r},a_{r}}(x)={\begin{cases}a_{l}&x\leqslant t_{l}\\1&t_{l}<x<t_{r}\\a_{r}&x\geqslant t_{r}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$	Нет	Нет	Нет
Обратный квадратный линейный корень (англ. Inverse square root linear unit, ISRLU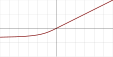)		$f(x)={\begin{cases}{\frac {x}{\sqrt {1+\alpha x^{2}}}}&x<0\\x&x\geqslant 0\end{cases}}$	$f'(x)={\begin{cases}\left({\frac {1}{\sqrt {1+\alpha x^{2}}}}\right)^{3}&x<0\\1&x\geqslant 0\end{cases}}$	$\left(-{\frac {1}{\sqrt {\alpha }}},\infty \right)$	$C^{2}$	Да	Да	Да
Адаптивная кусочно-линейная функция (англ. Adaptive piecewise linear, APL)		$f(x)=\max(0,x)+\sum _{s=1}^{S}a_{i}^{s}\max(0,-x+b_{i}^{s})$	$f'(x)=H(x)-\sum _{s=1}^{S}a_{i}^{s}H(-x+b_{i}^{s})$	$(-\infty ,\infty )$	$C^{0}$	Нет	Нет	Нет
SoftPlus		$f(x)=\ln(1+e^{x})$	$f'(x)={\frac {1}{1+e^{-x}}}$	$(0,\infty )$	$C^{\infty }$	Да	Да	Нет
Выгнутая тождественная функция (англ. Bent identity)		$f(x)={\frac {{\sqrt {x^{2}+1}}-1}{2}}+x$	$f'(x)={\frac {x}{2{\sqrt {x^{2}+1}}}}+1$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да
Cигмоидно-взвешенная линейная функция (англ. Sigmoid-weighted linear unit, SiLU)		$f(x)=x\cdot \sigma (x)$	$f'(x)=f(x)+\sigma (x)(1-f(x))$	$[\approx -0,28,\infty )$	$C^{\infty }$	Нет	Нет	Нет
SoftExponential		$f(\alpha ,x)={\begin{cases}-{\frac {\ln(1-\alpha (x+\alpha ))}{\alpha }}&\alpha <0\\x&\alpha =0\\{\frac {e^{\alpha x}-1}{\alpha }}+\alpha &\alpha >0\end{cases}}$	$f'(\alpha ,x)={\begin{cases}{\frac {1}{1-\alpha (\alpha +x)}}&\alpha <0\\e^{\alpha x}&\alpha \geqslant 0\end{cases}}$	$(-\infty ,\infty )$	$C^{\infty }$	Да	Да	Да, когда $\alpha =0$
Синусоида		$f(x)=\sin(x)$	$f'(x)=\cos(x)$	$[-1,1]$	$C^{\infty }$	Нет	Нет	Да
Sinc		$f(x)={\begin{cases}1&x=0\\{\frac {\sin(x)}{x}}&x\neq 0\end{cases}}$	$f'(x)={\begin{cases}0&x=0\\{\frac {\cos(x)}{x}}-{\frac {\sin(x)}{x^{2}}}&x\neq 0\end{cases}}$	$[\approx -0,217234,1]$	$C^{\infty }$	Нет	Нет	Нет
Гауссова		$f(x)=e^{-x^{2}}$	$f'(x)=-2xe^{-x^{2}}$	$(0,1]$	$C^{\infty }$	Нет	Нет	Нет

↑ Здесь, H является ступенчатой функцией Хевисайда.

↑ α является стохастической переменной, берущейся из равномерного распределения в момент обучения, значение которой фиксируется равным математическому ожиданию распределения в момент тестирования.

↑ ↑ ↑ Здесь $\sigma$ является логистической функцией.

Следующая таблица перечисляет функции активации, которые не являются функциями от одной свёртки x от предыдущего уровня или уровней:

Название	Уравнение	Производные	Область значений	Степень гладкости
Softmax	$f_{i}({\vec {x}})={\frac {e^{x_{i}}}{\sum _{j=1}^{J}e^{x_{j}}}}$    для i = 1, …, J	${\frac {\partial f_{i}({\vec {x}})}{\partial x_{j}}}=f_{i}({\vec {x}})(\delta _{ij}-f_{j}({\vec {x}}))$	$(0,1)$	$C^{\infty }$
Maxout	$f({\vec {x}})=\max _{i}x_{i}$	${\frac {\partial f}{\partial x_{j}}}={\begin{cases}1&j={\underset {i}{\operatorname {argmax} }}\,x_{i}\\0&j\neq {\underset {i}{\operatorname {argmax} }}\,x_{i}\end{cases}}$	$(-\infty ,\infty )$	$C^{0}$

↑  Здесь $\delta _{ij}$ обозначает символ Кронекера.

См. также

• Логистическая функция
• Выпрямитель (нейронные сети)
• Устойчивость (теория обучения)
• Softmax