Параллелепипед

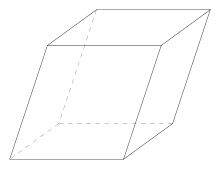
Параллелепипед

Параллелепи́пед (др.-греч. παραλληλ-επίπεδον от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, все грани которой являются параллелограммами.

Типы параллелепипеда

Прямоугольный параллелепипед

Различается несколько типов параллелепипедов:

• Наклонный — боковые грани не перпендикулярны основанию.
• Прямой — боковые грани перпендикулярны основанию.
• Прямоугольный — все грани являются прямоугольниками.
• Ромбоэдр — все грани являются равными ромбами.
• Куб — все грани являются квадратами.

Основные элементы

• Две грани параллелепипеда, не имеющие общего ребра, называются «противоположными гранями»; например, грань AA₁D₁D противоположна грани BB₁C₁C
• Две грани параллелепипеда, имеющие общее ребро, называются «смежными гранями»; например, грань AA₁D₁D смежна грани DD₁C₁C (имеется общее ребро DD₁)
• Две вершины параллелепипеда, не принадлежащие одной грани, называются «противоположными вершинами»; например, вершина A противоположна вершине C₁ (а вершина A не противоположна вершине C, поскольку они принадлежат одной грани ABCD)
• Отрезок, соединяющий противоположные вершины, называется «диагональю параллелепипеда»; например отрезок AC₁
• Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют «измерениями прямоугольного параллелепипеда»; например длины рёбер AD, DC и DD₁ — имеют общую вершину D и являются измерениями прямоугольного параллелепипеда ABCDA₁B₁C₁D₁

Свойства

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы

Прямой параллелепипед

Площадь боковой поверхности S_б = Р_о⋅h, где Р_о — периметр основания, h — высота.

Площадь полной поверхности S_п = S_б + 2S_о, где S_о — площадь основания.

Объём V = S_о⋅h.

Прямоугольный параллелепипед

Основная статья: Прямоугольный параллелепипед

Площадь боковой поверхности S_б = 2c(a + b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда.

Площадь полной поверхности S_п = 2(ab + bc + ac).

Объём V = abc, где a, b, c — измерения прямоугольного параллелепипеда.

Куб

Площадь поверхности $S=6a^{2}$.

Объём $V=a^{3}$, где $a$ — ребро куба.

Произвольный параллелепипед

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения.

Если координаты четырёх вершин параллелепипеда, не принадлежащих одной грани, имеют целочисленные координаты, то объём этого параллелепипеда есть целое число.

В математическом анализе

В математическом анализе под n-мерным прямоугольным параллелепипедом $B$ понимают множество точек $x=(x_{1},\ldots ,x_{n})$ вида $B=\{x|a_{1}\leqslant x_{1}\leqslant b_{1},\ldots ,a_{n}\leqslant x_{n}\leqslant b_{n}\}$

Сечение параллелепипеда плоскостью

В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.

См. также

• Параллелепипед Эйлера
• Параллелепипед Френеля

Ссылки

• Прямоугольный параллелепипед Архивная копия от 21 февраля 2020 на Wayback Machine