Золотое сечение

Иррациональные числа ζ(3) — ρ — √2 — √3 — √5 — ln 2 — φ,Φ — ψ — α,δ — e — eπ и π
Система счисления	Оценка числа Φ
Десятичная	1.6180339887498948482…
Двоичная	1.1001111000110111011…
Шестнадцатеричная	1.9E3779B97F4A7C15F39…
Шестидесятеричная	1; 37 04 55 20 29 39 …
Рациональные приближения	3/2; 5/3; 8/5; 13/8; 21/13; 34/21; 55/34; 89/55; … $F_{n+1}/F_{n}$, где $F_{n}$ — числа Фибоначчи (перечислено в порядке увеличения точности)
Непрерывная дробь	$1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}$

1,6180339887 4989484820 4586834365 6381177203 0917980576 2862135448 6227052604 6281890244 9707207204 1893911374 8475408807 5386891752 1266338622 2353693179 3180060766 7263544333 8908659593 9582905638 3226613199 2829026788 0675208766 8925017116 9620703222 1043216269 5486262963 1361443814 9758701220 3408058879 5445474924 6185695364 8644492410 4432077134 4947049565 8467885098 7433944221 2544877066 4780915884 6074998871 2400765217 0575179788 3416625624 9407589069 7040002812 1042762177 1117778053 1531714101 1704666599 1466979873 1761356006 7087480710 1317952368 9427521948 4353056783 0022878569 9782977834 7845878228 9110976250 0302696156 1700250464 3382437764 8610283831 2683303724 2926752631 1653392473 1671112115 8818638513 3162038400 5222165791 2866752946 5490681131 7159934323 5973494985 0904094762 1322298101 7261070596 1164562990 9816290555 2085247903 5240602017 2799747175 3427775927 7862561943 2082750513 1218156285 5122248093 9471234145 1702237358 0577278616 0086883829 5230459264 7878017889 9219902707 7690389532 1968198615 1437803149 9741106926 0886742962 2675756052 3172777520 3536139362

---

Первая тысяча знаков значения Φ.

Золото́е сече́ние (золота́я пропо́рция, иначе: деле́ние в кра́йнем и сре́днем отноше́нии, гармони́ческое деление) — отношение частей и целого, при котором отношения частей между собой и наибольшей части к целому равны. Такие отношения наблюдаются в природе, открыты в науке и соблюдаются в искусстве. На «золотых отрезках» основываются различные системы и способы пропорционирования в архитектуре. Соотношение двух величин $a$ и $b$, при котором бо́льшая величина относится к меньшей так же, как сумма этих величин к бо́льшей, то есть ${\frac {a}{b}}={\frac {a+b}{a}}$, является универсальным. Отсюда название, которое впервые появилось в эпоху Возрождения, в частности в трактате францисканского монаха, математика Луки Пачоли Божественная пропорция (лат. De Divina Proportione (1509 год), но закономерность подобных отношений была известна гораздо раньше: в Древней Месопотамии, Египте и античной Греции.

Исторически в древнегреческой математике золотым сечением именовалось деление отрезка $AB$ точкой $C$ на две части так, что бо́льшая часть относится к меньшей, как весь отрезок к большей: ${\frac {BC}{AC}}={\frac {AB}{BC}}.$ Это понятие было распространено не только на отрезки, но и на произвольные величины.

Число, равное отношению $a/b,$ обычно обозначается прописной греческой буквой $\Phi$ (фи), в честь древнегреческого скульптора и архитектора Фидия, реже — греческой буквой $\tau$ (тау).

Из исходного равенства (например, принимая $AB$ за 1, $AC$ за неизвестную переменную $y$ и $BC$ за $x,$ и решая получившуюся систему уравнений $x+y=1;\ x/y=1/x$) получается квадратное уравнение:

$$1+{1 \over x}=x\Longleftrightarrow x^{2}-x-1=0,$$

а после его решения и число: $\Phi ={\frac {1+{\sqrt {5}}}{2}}.$

Обратное число, обозначаемое строчной буквой $\varphi$,

$\varphi ={\frac {1}{\Phi }}={\frac {{\sqrt {5}}-1}{2}}=e^{-0,2i\pi }+e^{0{,}2i\pi }=e^{-0{,}2\ln -1}+e^{0{,}2\ln -1}=(-1)^{-0{,}2}+(-1)^{0{,}2}={\frac {1}{\sqrt[{5}]{-1}}}+{\sqrt[{5}]{-1}}=2{\mathfrak {R}}({\sqrt[{5}]{-1}})\approx 0{,}61803$

Легко видеть, что

$\varphi =\Phi -1.$

Число $\Phi$ называется также золотым числом.

Для практических целей обычно ограничиваются приблизительным значением $\Phi \approx 1{,}618$ или $\Phi \approx 1{,}62.$ В процентах округлённое значение золотое сечение — это деление некоторой величины в отношении 62 % и 38 %.

Иллюстрация к определению

Золотое сечение имеет множество замечательных свойств (например, $\Phi$² = $\Phi$ + 1), но, кроме того, ему приписывают и многие вымышленные свойства.

История

В дошедшей до нас античной литературе деление отрезка в крайнем и среднем отношении (ἄκρος καὶ μέσος λόγος) впервые встречается в «Началах» Евклида (около 300 лет до н. э.), где оно применяется для построения правильного пятиугольника.

Лука Пачоли, современник и друг Леонардо да Винчи, усматривал в этой пропорции «божественную суть», выражающую триединство Бога Отца, Сына и Святого Духа.

Неизвестно точно, кто и когда именно впервые ввёл в обращение термин «золотое сечение». Несмотря на то, что некоторые авторитетные авторы связывают появление этого термина с Леонардо да Винчи в XV веке или относят появление этого термина к XVI веку, самое раннее употребление этого термина находится у Мартина Ома в 1835 году, а именно в примечании ко второму изданию его книги «Чистая элементарная математика», в котором Ом пишет, что это сечение часто называют золотым сечением (нем. goldener Schnitt). Из текста этого примечания следует, что Ом не придумал этот термин сам, хотя некоторые авторы утверждают обратное. Тем не менее, исходя из того, что в первом издании своей книги Ом уже не употреблял этот термин, Роджер Герц-Фишлер делает вывод о том, что этот термин, возможно, появился в первой четверти XIX века. Марио Ливио считает, что он получил популярность в устной традиции около 1830 года. В любом случае именно после Ома термин стал распространён в немецкой математической литературе.

Математические свойства

• $\Phi$ — иррациональное алгебраическое число, положительное решение квадратного уравнения $x^{2}-x-1=0,$ из которого, в частности, следуют соотношения:

  $\Phi ^{2}-\Phi =1,$

  $\Phi \cdot (\Phi -1)=1.$

• $\Phi$ представляется через тригонометрические функции (см. «Тригонометрические константы»):
  • $\Phi =2\cos {\frac {\pi }{5}}=2\cos 36^{\circ }.$
  • $\Phi =2\sin(3\pi /10)=2\sin 54^{\circ }.$

• Если угол между диагональю и меньшей стороной прямоугольника, относящейся к большей стороне как 1:2, поделить пополам, то по формуле тангенса половинного угла получится соотношение:

${\frac {1}{\Phi }}=\varphi =\operatorname {tg} \left({\frac {\operatorname {arctg} (2)}{2}}\right)={\frac {2}{1+{\sqrt {1+2^{2}}}}}={\frac {2}{1+{\sqrt {5}}}}={\frac {{\sqrt {5}}-1}{2}}.$

• $\Phi$ представляется в виде бесконечной цепочки квадратных корней:

  $\Phi ={\sqrt {1+{\sqrt {1+{\sqrt {1+{\sqrt {1+\dots }}}}}}}}~.$

• $\Phi$ представляется в виде бесконечной цепной дроби

  $\Phi =1+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{1+\dots }}}}}},$

подходящими дробями которой служат отношения последовательных чисел Фибоначчи ${\frac {F_{n+1}}{F_{n}}}$. Таким образом,

• $\Phi =\lim _{n\to \infty }{\frac {F_{n+1}}{F_{n}}}.$

• Мера иррациональности $\Phi$ равна 2.

Отрезание квадрата от прямоугольника, имеющего золотую пропорцию

• Отрезав квадрат от прямоугольника, построенного с золотой пропорцией, мы получаем новый, уменьшенный прямоугольник с тем же отношением сторон $\Phi =a/b,$ что и у исходного прямоугольника $\Phi =(a+b)/a.$
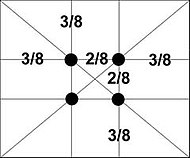
• Продолжая отрезать квадраты против часовой стрелки получим согласно рисунку координаты предельной точки $(a+b){\frac {1}{1-\varphi ^{4}}},\;a{\frac {1-\varphi ^{4}-\varphi ^{5}}{1-\varphi ^{4}}}.$ Более того, это точка будет лежать на пересечении диагоналей первого и второго прямоугольников.

Золотое сечение в пятиконечной звезде

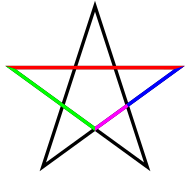
• В правильной пятиконечной звезде каждый отрезок делится другим отрезком, пересекающим его, в золотом сечении. На приведённом рисунке отношения красного отрезка к зелёному, зелёного к синему и синего к пурпурному равны $\Phi .$ Кроме того, отношение красного отрезка к расстоянию между любыми соседними вершинами звезды, которое равно зелёному отрезку, также равно $\Phi .$

Построение золотого сечения

• Геометрическое построение. Золотое сечение отрезка $AB$ можно построить следующим образом: в точке $B$ проводят перпендикуляр к $AB,$ откладывают на нём отрезок $BC,$ равный половине $AB,$ на отрезке $AC$ откладывают отрезок $CD,$ равный $BC,$ и наконец на отрезке $AB$ откладывают отрезок $AE,$ равный $AD.$ Тогда:

$\Phi ={\frac {|AB|}{|AE|}}={\frac {|AE|}{|BE|}}.$

Другой способ построить отрезок, равный по длине числу золотого сечения

• Другой способ построить отрезок, равный по длине числу золотого сечения, — это начертить квадрат ABCD со стороной 1, после этого одну из сторон, например сторону AD, разделить точкой E пополам, так что AE = DE = 1/2, далее от точки B или C до точки E провести гипотенузу треугольника АВЕ или DCE. Согласно теореме Пифагора $BE=CE={\tfrac {\sqrt {5}}{2}}$. Затем провести дугу с центром в точке Е от точки В или точки С до прямой, где лежит сторона AD и точка пересечения где будет называться Н. Стороны BE, СЕ и ЕН равны как радиусы окружности. Так как АН = АЕ + ЕН, то отрезок АН длины $\Phi$ и будет результатом. Кроме того, поскольку DH = EH – ED, отрезок DH будет иметь длину $\varphi$.

• Отношение диагонали правильного пятиугольника к стороне равно золотому сечению.
• Значения дробной части чисел $\Phi ,$ ${\frac {1}{\Phi }}$ и $\Phi ^{2}$ в любой системе счисления будут равны.
• $\sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n^{2}{\binom {2n}{n}}}}=2\ln ^{2}\varphi ,$

где ${\tbinom {2n}{n}}$ — биномиальный коэффициент, тогда как $\sum _{n=1}^{\infty }{\frac {1}{n^{2}{\binom {2n}{n}}}}={\frac {\pi ^{2}}{18}}$

Золотое сечение в физике, геометрии, химии

Общее сопротивление этой бесконечной цепи равно $\Phi r$

Золотое число возникает в разных задачах, в том числе в физике. Например, бесконечная электрическая цепь, приведённая на рисунке, имеет общее сопротивление (между двумя левыми концами) $\Phi \cdot r.$

Отношение амплитуд колебаний и частот ~Ф

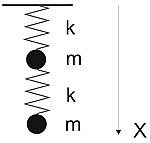
Существуют колебательные системы, физические характеристики которых (отношения частот, амплитуд и др.) пропорциональны золотому сечению. Самый простой пример — система из двух шариков, соединённых последовательно пружинами одинаковой жёсткости (см. рисунок).

Более сложные примеры механических колебаний и их обобщений рассматриваются в этой^{[прояснить]} же книге, в главе «Обобщения одной простой задачи по механике». В книге приведено много примеров проявления и применения золотого сечения в различных областях наук — небесной механике, физике, геофизике, биофизике, физической химии, биологии, Физиологии.

Золотое сечение тесно связано с симметрией пятого порядка, наиболее известными трёхмерными представителями которой являются додекаэдр и икосаэдр. Можно сказать, что всюду, где в структуре проявляются додекаэдр, икосаэдр или их производные, там в описании будет появляться и золотое сечение. Например, в пространственных группировках атомов бора: В-12, В-50, В-78, В-84, В-90, …, В-1708, имеющих икосаэдрическую симметрию. Молекула воды, у которой угол между связями Н-О равен 104,7⁰, то есть близок к 108 градусам (равен углу в правильном пятиугольнике), может соединяться в плоские и трехмерные структуры с симметрией пятого порядка. Так, в разреженной плазме был обнаружен ион Н⁺(Н₂0)₂₁, который представляет собой ион Н₃0⁺, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. В 80-х годах XX века были получены клатратные соединения, содержащие гексааквакомплекс кальция, окруженный 20 молекулами воды, расположенными в вершинах додекаэдра. Есть и клатратные модели воды, в которых обыкновенная вода отчасти состоит из молекул воды, соединённых в структуры с симметрией пятого порядка. Такие структуры могут состоять из 20, 57, 912 молекул воды.

Золотое сечение и гармония в искусстве

Иллюстрация композиционного значения золотого сечения.

Некоторые из утверждений в доказательство гипотезы знания древними правила золотого сечения:

• Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона близки к золотому сечению.
• По мнению Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д.
• Использование пропорции «золотого сечение» в пропорциях канонов человеческого тела, судя по историческим документам^{[каким?]}, вызывает очень большие сомнения. Начиная с работы Адольфа Цейзинга сформировалась целая система мифов о «золотом сечении».

Один из типов мозаики Пенроуза

Возможные примеры сознательного использования

Начиная с Леонардо да Винчи, многие художники сознательно использовали пропорции «золотого сечения». Российский зодчий И. В. Жолтовский использовал золотое сечение в своих проектах.

Иоганн Себастьян Бах в своей трёхголосной инвенции E-dur № 6 BWV 792 использовал двухчастную форму, в которой соотношение размеров частей соответствует пропорциям золотого сечения. 1 часть — 17 тактов, 2 часть — 24 такта (небольшие несоответствия выравниваются за счёт ферматы в 34 такте).

Современными примерами применения золотого сечения может служить мозаика Пенроуза и пропорции государственного флага Того.

Золотое сечение в биологии и медицине

Золотое сечение в природе

Живые системы также обладают свойствами, характерными для «золотого сечения». Например: пропорции тел, спиральные структуры или параметры биоритмов и др.

См. также

• Божественная пропорция
• Диагональный метод
• Золотая спираль
• Золотой прямоугольник
• Пифагорейский пентакл
• Пропорционирование
• Фибоначчиева система счисления
• Правило третей
• Метод золотого сечения
• Сверхзолотое сечение
• Пластическое число
• Золотой угол
• Канон (искусство)
• Модулор
• Числа Фибоначчи
• Обобщение чисел Фибоначчи
• Обобщённое золотое сечение

Литература

на русском языке

• Аракелян Г. Б. Математика и история золотого сечения. — М.: Логос, 2014, 404 с. — ISBN 978-5-98704-663-0.
• Бендукидзе А. Д. Золотое сечение Архивная копия от 11 октября 2004 на Wayback Machine «Квант» № 8, 1973.
• Васютинский Н. А. Золотая пропорция. — М.: Молодая гвардия, 1990. — 238[2]c. — (Эврика).
• Власов В. Г. Золотое сечение, или Божественная пропорция // Власов В. Г. Новый энциклопедический словарь изобразительного искусства: В 10 т. — Т.3. — СПб.: Азбука-Классика, 2005. — С. 725—732.
• Власов В. Г. Приемы гармонизации пространства в классической архитектуре // Власов В. Г. Искусство России в пространстве Евразии. — Т.3. Классическое искусствознание и «русский мир». — СПб.: Дмитрий Буланин, 2012. — С. 156—192.
• Мазель Л. А. Опыт исследования золотого сечения в музыкальных построениях в свете общего анализа форм // Музыкальное образование. — 1930. — № 2. — С. 24—33.
• Сабанеев Л. Л. Этюды Шопена в освещении закона золотого сечения. Опыт позитивного обоснования законов формы // Искусство. — 1925. — № 2. — С. 132—145; 1927. — № 2—3. — С. 32—56.
• Шевелев И. Ш., Марутаев М. А., Шмелев И. Л. Золотое сечение. Три взгляда на природу гармонии (рус.). — М.: Стройиздат, 1990. — 343 с. — ISBN 5-274-00197-1.
• Шевелев И. Ш. Геометрическая гармония. Опыт исследования пропорциональности в архитектуре (рус.). — Кострома, 1963. — 107 с.
• Шмигевский Н. В. Формула совершенства // Страна знаний. — 2010. — № 4. — С. 2—7.

на других языках

• Mario Livio. The Golden Ratio: The Story of PHI, the World's Most Astonishing Number. — Crown/Archetype, 2008. — 303 с. — ISBN 9780307485526. Архивная копия от 31 марта 2019 на Wayback Machine Русский перевод в

Марио Ливио. φ – Число Бога. Золотое сечение – формула мироздания. — Litres, 2015-04-17. — 481 с. — ISBN 9785457762732. Архивная копия от 24 июня 2016 на Wayback Machine

• Roger Herz-Fischler. A Mathematical History of the Golden Number. — Courier Corporation, 2013. — 228 с. — ISBN 9780486152325. Архивная копия от 2 июля 2016 на Wayback Machine

Ссылки

• Белянин В. С., «Владел ли Платон кодом золотой пропорции? Анализ мифа»
• Радзюкевич А. В., К вопросу о научном изучении пропорций в архитектуре и искусстве Архивная копия от 3 апреля 2015 на Wayback Machine.
• Радзюкевич А. В., Критический анализ Адольфа Цейзинга — основоположника гипотезы «золотого сечения». Архивная копия от 19 декабря 2014 на Wayback Machine
• Статья о золотом сечении в изобразительном искусстве, Золотое сечение в изобразительном искусстве
• J. J. O'Connor, E. F. Robertson. Golden ratio  (неопр.). MacTutor History of Mathematics archive. School of Mathematics and Statistics, University of St Andrews, Scotland. Дата обращения: 13 ноября 2015. Архивировано 25 июля 2015 года.
• Функция Фибоначчи Архивная копия от 30 октября 2020 на Wayback Machine в Wolfram alpha