Математика и архитектура

Материал из Википедии — свободной энциклопедии
Перейти к навигации Перейти к поиску
«Корнишон»[1], Небоскрёб Мэри-Экс, Лондон, завершен в 2003, с использованием параметрического проектирования[en]* тела вращения.
Кандарья-Махадева, Группа храмов Кхаджурахо[en], Индия, является примером религиозной архитектуры с похожей на фракталы структурой, которая имеет многие части, напоминающие весь объект в целом. 1030[2]

Как и в других видах искусств, в архитектуре используются математика. Даже если отбросить необходимость этого для проектирования здания архитекторам не обойтись без знания геометрии при определении пространственной формы сооружения. Начиная со времён пифагореизма (VI в. до н. э.), для создания архитектурных форм было необходимо следовать правилам гармонии, то есть проектирование зданий и окружающего ландшафта происходило согласно математическим и эстетическим принципам, наряду с религиозными. Элементы, подобные математическим объектам, используют при облицовке зданий, например, замощении. Математические расчёты также необходимы для достижения экологических целей, например, минимизации скорости ветра около основания высотных зданий.

В Древнем Египте, Древней Греции, Индии и исламском мире строения, включая пирамиды, храмы, мечети, дворцы и мавзолеи, проектировались со специфичными пропорциями по религиозным причинам[3][4]. В исламской архитектуре геометрические формы и геометрические мозаичные орнаменты[en] использовали для облицовки зданий, как внутри, так и снаружи[5][6]. Некоторые индуистские дворцы имеют подобные фракталам структуры, в которых часть подобна целому, олицетворяя бесконечность в индуистской космологии[2][7]. В архитектуре Китая, тулоу (провинция Фуцзянь)— это круглые структуры коллективной защиты. В XXI веке математические орнаменты снова начали использоваться для облицовки общественных зданий[8][9][10][11].

В архитектуре эпохи Возрождения симметрия и пропорции играли важную роль и были подчёркнуты архитекторами того времени. Это можно увидеть в творениях Леона Баттиста Альберти, Себастьяно Серлио и Андреа Палладио, находившихся под влиянием трактата «Десять книг об архитектуре» Витрувия. В конце XIX века Владимир Шухов в России и Антонио Гауди в Испании положили начало использованию гиперболоидных конструкций[12][13][14]. К примеру, при проектировании Храма Святого Семейства Гауди использовал гиперболические параболоиды, мозаики, арки с очертанием обратной цепной линии[en], катеноиды, геликоиды и линейчатые поверхности[12][13][14]. В XX веке в архитектурном модернизме и деконструктивизме широко использовались геометрические формы для получения запланированных визуальных эффектов[15][16]. Понятие «минимальная поверхность» было использовано при проектировании купола Денверского Международного аэропорта в виде горных вершин или палаток. Ричард Бакминстер Фуллер положил начало применению усиленных тонкостенных оболочек, известных как геодезические купола[17].

Связанные области[править | править код]

В эпоху возрождения предполагалось, что архитекторы, подобные Леону Баттиста Альберти, компетентны во многих дисциплинах, включая арифметику и геометрию.

Архитекторы Майкл Освальд и Ким Уильямс, анализируя связь между архитектурой и математикой, отметили, что по общему пониманию эти две области связаны слабо, поскольку архитектура относится к практическому строительству зданий, в то время как математика является чистой теорией, изучающей числа и другие абстрактные объекты[18]. Но, как они утверждают, эти две области сильно связаны, и связаны они ещё с античности. В Древнем Риме Витрувий описывал архитектора как человека, знающего достаточно большой объём других дисциплин, главным образом геометрию, что позволяет ему контролировать квалифицированных ремесленников в других сферах деятельности, таких как каменщики и плотники[19]. То же самое относится к средним векам, когда выпускники высших заведений учили арифметику, геометрию и эстетику наравне с базовыми курсами грамматики, логики и риторики (тривиум) в элегантных аудиториях, сделанных строителями, которые руководили многими рабочими.[источник не указан 1804 дня] Строителям на вершине их профессии давался титул архитектора или инженера. В эпоху Возрождения, квадривиум арифметики, геометрии, музыки и астрономии стал дополнительной программой, которую должны были знать люди эпохи Возрождения, такие как Леон Баттиста Альберти. Аналогично, в Англии, сэр Кристофер Рен, сегодня известный как архитектор, был первоначально знаменитым астрономом[20].

Уильям и Оствальд, рассматривая позднее взаимодействие математики и архитектуры с 1500 года, согласно подходу немецкого социолога Теодора Адорно, определили три тенденции архитектуры, а именно — революционная, предлагающая полностью новые идеи, реакционная, противящаяся нововведениям, и художники, возрождающие традиции[en], на самом деле идущие назад[21]. Утверждали, что архитекторы избегали использования математики для получения вдохновения во времена возрождения традиций. Это может объяснить, почему во времена возрождения традиций, таких как неоготика в XIX веке в Англии, архитектура имела малую связь с математикой. Также они заметили, что в таких направлениях как итальянский маньеризм примерно с 1520 по 1580 год, или барокко и палладианство периода XVII века, математика мало принималась во внимание. Для контраста революционные движения ранних годов XX века, такие как футуризм и конструктивизм, активно отбрасывали старые идеи, использовали математику и вели к модернизму в архитектуре. К концу XX века фрактальная геометрия была быстро подхвачена архитекторами, как и непериодичные замощения, позволяющие осуществить интересные и привлекательные облицовки зданий [8].

Архитекторы используют математику по нескольким причинам, даже если оставить в стороне необходимость использования математики в проектировании зданий[en][22]. Во-первых, они используют геометрию, чтобы определять пространственные формы здания[23]. Во-вторых, они используют математику для проектирования форм, считающихся прекрасными или гармоничными[24]. Со времён пифагореизма с их религиозной философией чисел[25], архитекторы Древней Греции, Древнего Рима, исламского мира и итальянского Ренессанса выбрали пропорции строительного окружения — зданий и их окружения — согласно эстетическим и религиозным принципам[26][27][28][5]. В-третьих, они могут использовать математические объекты, такие как замощения, для украшения зданий[29][30]. В-четвёртых, они могут использовать математику в виде компьютерного моделирования для достижения экологических целей, таких как минимизация вихрей при огибании основания высоких зданий [1].

Гармония пространственных форм[править | править код]

Светская эстетика[править | править код]

Древний Рим[править | править код]

План греческого дома Витрувия
Витрувий[править | править код]
Подробное рассмотрение темы: Витрувий, Виртувианов модуль и Десять книг об архитектуре
Внутренний вид Пантеона (картина Джованни Паоло Панини, 1758)

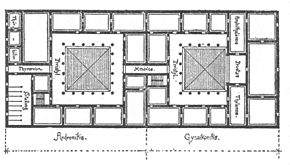
Влиятельный древнеримский архитектор Витрувий утверждал, что планирование здания, такого как храм, зависит от двух качеств: пропорций и симметрии. Пропорции отвечают за гармоничное отношение каждой части здания ко всем остальным. Симметрия в понимании Витрувия означает нечто более близкое к модульности, чем к зеркальной симметрии, так как это относится к сборке (модульных) частей в единое строение. В базилике в городе Фано использованы отношения малых целых чисел, в частности, треугольных чисел (1, 3, 6, 10, …) как пропорции структуры (витрувиановых) модулей[en][a]. Так, ширина базилики относится к длине как 1:2, нефы вокруг неё имеют такую же высоту, как и ширину, 1:1, толщина колонн составляет пять футов, а высота — пятьдесят футов, 1:10[26].

План Пантеона

Витрувий назвал три свойства, требуемые от архитектуры, в трактате Десять книг об архитектуре (XV век до нашей эры) — прочность, практичность и приятный вид. Эти свойства можно использовать как категории для классификации способов использования математики в архитектуре. Прочность охватывает использование математики для обеспечения устойчивости зданий, поскольку математические средства используются для проектирования и поддержки конструкций, например, для обеспечения стабильности и качественного моделирования. Практичность достигается отчасти путём эффективного применения математики, обосновывая и анализируя пространственные и другие связи при проектировании. Приятный вид является атрибутом здания, являющимся воплощением математических связей в здании. Он включает эстетику, чувственные и интеллектуальные свойства[32].

Пантеон[править | править код]
Основная статья: Пантеон (Рим)

Сохранившийся невредимым Пантеон в Риме иллюстрирует классическую структуру римских строений, пропорций и украшений. Основной структурой является купол, высшую точку которого оставляли открытой в качестве круглого окулюса, пропускающего свет. Пантеон с фасада снабжён колоннадой с треугольным фронтоном. Высота окулюса и диаметр внутреннего круга (43,3 метра) совпадают так, что внутренняя часть полностью помещается в куб[33]. Эти размеры будут более понятны, если обратить внимание на список древнеримских единиц (купол имеет диаметр 150 римских футов[en]*[b]). Окулюс равен 30 римским футам в диаметре, дверной проём имеет высоту 40 римских футов[34]. Пантеон остаётся крупнейшим в мире бетонным сводом без арматуры[35].

Возрождение[править | править код]

Подробное рассмотрение темы: Архитектура Возрождения
Фасад базилики Санта-Мария-Новелла, Флоренция, 1470. Бордюр (с квадратами) и выше принадлежит Леона Баттиста Альберти.

Первым трактатом эпохи возрождения по архитектуре был трактат Леона Баттиста Альберти (1450) On the Art of Building[en] (Об искусстве строительства). Изданный в 1485 году, трактат стал первой печатной книгой по архитектуре. Он частично базировался на книге Витрувия Десять книг об архитектуре и пифагоровой арифметике. Альберти начинает с куба и выводит из него пропорции. Так, диагонали грани дают отношение 1:√2, а диаметр сферы, описанный вокруг куба, имеет отношение 1:√3[36][37]. Альберто также описывает открытие Филиппо Брунеллески линейной перспективы[en], разработанной для планирования зданий, которые выглядят вполне пропорционально, если рассматривать с удобного расстояния[5].

Архитектурная перспектива декораций Себастьяно Серлио, 1569[38]

Следующим важным текстом была книга Себастьяна Серлио Regole generali d’architettura (Основные правила архитектуры). Первый том книги вышел в Венеции в 1537 году. Том 1545 года (книги 1 и 2) охватывают геометрию и перспективу[en]. Два метода построения перспективы Серлио были ошибочными, но это не остановило широкое использование книги[39].

План и профиль виллы Пизани[en] Андреа Палладио

В 1570 году Андреа Палладио опубликовал авторитетные I quattro libri dell’architettura (Четыре книги об архитектуре) в Венеции. Эти книги получили широкое распространение и продвигали идеи итальянского возрождения в Европе при содействии сторонников идей, таких как английский дипломат Генри Уоттон, выпустивший в 1624 году трактат «Элементы архитектуры»[40]. Пропорции каждого помещения внутри особняка вычислялись с помощью простых математических отношений, таких как 3:4 и 4:5, и различные помещения внутри дома были связаны этими соотношениями. Ранние архитекторы использовали эти формулы для балансирования симметрии фасада. Однако проекты Палладио относились, как правило, к квадратным особнякам[41]. Палладио допускал ряд отношений в Quattro libri, утверждая[42][43]:

Имеется семь типов помещений, наиболее прекрасных и хорошо пропорциональных. Это круглые, хотя они редки, квадратные или их длина равна диагонали квадрата ширины, ширине с третью, ширине с половиной, ширине и две трети и две ширины.[c]

В 1615 году Винченцо Скамоцци опубликовал трактат L’Idea dell’Architettura Universale (Идея Универсальной Архитектуры)[44]. Он попытался соотнести планирование городов и зданий с идеями Витрувия, пифагорейцев и более свежих идей Палладио[45].

Девятнадцатый век[править | править код]

Гиперболоидная решётка маяка Владимира Шухова, Украина, 1911

Гиперболоидные конструкции начали использоваться с конца XIX века Владимиром Шуховым для мачт, маяков и градирен. Несмотря на экономное использование материала при производстве, конструкции Шухова довольно прочны. Первая гиперболоидная башня Шухова была представлена на выставке в Нижнем Новгороде в 1896 году[46][47][48].

Двадцатый век[править | править код]

Подробное рассмотрение темы: Архитектурный модернизм и Архитектура XXI века
Общество художников Де Стейл — заходящие друг за друга и пересекающиеся плоскости — Дом Шрёдер, 1924

В движении начала XX века «архитектурный модернизм», у истоков которого лежал русский [d] конструктивизм[49], использовалась евклидова геометрия. В движении общества художников Де Стейл горизонталь и вертикаль рассматриваются как составляющие вселенной. Архитектурные формы заключаются в помещении этих двух направлений вместе с использованием плоскости крыш, плоскостей стен и балконов, которые либо заходят одна за другую, либо пересекаются, как в доме Шрёдер, построенном в 1924 году Герритом Ритвельдом[50].

Мак и перечница (биомитетика), иллюстрации из книги Die Pflanze als Erfinder (Растение как изобретатель) Рауля Генриха Франсе[en], 1920

Архитекторы модернизма были свободны в использовании кривых наравне с плоскостями. Станция лондонской подземки в Арнос Гроув[en] Чарльза Холдена 1933 года имеет круглый кирпичный кассовый зал с плоским бетонным полом[51]. В 1938 году художник из высшей школы строительства и художественного конструирования Баухаус Ласло Мохой-Надь заимствовал семь биотехнических элементов Рауля Генриха Франсе[en]: кристалл, сфера, конус, плоскость, (кубовидная) лента, (цилиндрический) стержень и спираль в качестве базовых строительных архитектурных блоков, навеянных природой[52][53].

Ле Корбюзье предложил антропометрический масштаб пропорций в архитектуре «модулор» — систему пропорций, основанную на высоте человека[54]. В церкви Нотр-Дам-дю-О (Ле Корбюзье, 1955 года) используются кривые произвольной формы, не описываемые математическими формулами[e]. Конструкция имеет только большие масштабы — нет иерархии меньших масштабов, а потому никаких фрактальных размерностей. То же самое имеет место для других знаменитых зданий XX века, таких как Сиднейский оперный театр, Денверский Международный аэропорт и Музей Гуггенхейма в Бильбао[15].

Мнения об архитектуре XXI века[en] 90 ведущих архитекторов, которые участвовали в опросе о мировой архитектуре[en] 2010 года, крайне расходятся. Лучшим считается Музей Гуггенхейма в Бильбао Фрэнка Гери[55].

Минимальная поверхность тканевой крыши[en] Денверского Международного аэропорта, законченного в 1995, напоминают снежные горы Колорадо и палатки типи коренных народов США.

Здание терминала Международного аэропорта Дэнвера, построенного в 1995 году, имеет тканевую крышу[en], поддерживаемую в состоянии минимальной поверхности (то есть её средняя кривизна равна нулю) стальными тросами. Здание напоминает снежные вершины Колорадо и палатки типи коренных народов США (часто их неверно называют вигвамами)[56].

Архитектор Ричард Бакминстер Фуллер прославился благодаря созданию крепких тонкостенных структур, более известных как геодезические купола. Купол Биосферы в Монреале имеет высоту 61 метр, а его диаметр равен 76 метрам[17].

Сиднейский оперный театр имеет крышу, состоящую из взмывающих белых сводов, напоминающих паруса корабля. Чтобы сделать возможным построение из стандартных компонентов, своды составлены из треугольных секций сферической оболочки одинакового радиуса. Это требовало соблюдения одинаковой кривизны в любом направлении[57].

Движение конца XX века деконструктивизм создаёт обдуманный беспорядок, который Никос Салингарос в книге A Theory of Architecture (Теория архитектуры) называет случайными формами[58] высокой сложности[59]. Беспорядок создаётся непараллельными стенами, наложенными решётками и сложными двумерными поверхностями, как в концертном зале имени Уолта Диснея (архитектор Фрэнк Гери) и музее Гуггенхейма в Бильбао[60][61]. До XX века студенты архитектурных институтов обязаны были изучать основы математики. Салингарос утверждает, что первый «чрезвычайно упрощённый, политически мотивированный» модернизм, а затем «антинаучный» деконструктивизм эффективно отделили архитектуру от математики. Он убеждён, что эта «отмена математических значений» губительна, так как «повсеместная эстетика» нематематической архитектуры ведёт людей «к отказу от математической информации в окружающей среде города». Он утверждает, что это имеет негативный эффект на общество[15].

Религиозные принципы[править | править код]

Древний Египет[править | править код]

Подробное рассмотрение темы: Древнеегипетские погребальные обряды
Древнеегипетские пирамиды в Гизе имеют математические пропорции, случайно или намеренно.
Отношения основания к гипотенузе (b: a) для пирамид подобных пирамиде Хеопса, могут быть: 1:φ (треугольник Кеплера), 3:5 (треугольник 3-4-5[en]) или 1:4/π

Пирамиды Древнего Египта были погребениями, построенными с преднамеренно выбранными пропорциями, но с какими именно — до сих пор непонятно. Лицевой угол составляет около 51°85’ и отношение наклонной высоты на середину основания равно 1,619, что на 1 % меньше золотого сечения. Если это был метод расчёта, из этого следовало бы использование треугольника Кеплера (угол 51°49’)[62][63]. Однако более вероятно, что наклон пирамиды выбирался исходя из треугольника 3-4-5[en] (угол 53°8’), известного из папируса Ахмеса (1650—1550 года до н. э.), или из треугольника, отношение основания которого к гипотенузе составляет 1:4/π (угол 51°50’)[64].

Часто констатируется использование треугольника 3-4-5 для построения прямых углов, например, для планирования основания пирамиды, и подразумеваемое знание теоремы Пифагора [3]. Сначала это предположил историк Мориц Бенедикт Кантор в 1882 году[3]. Известно, что прямые углы были построены в Древнем Египте точно[3] и землемеры того времени использовали верёвки с узлами[en] для измерения [3]. Ещё Плутарх записал в сочинении Об Исиде и Осирисе (около 100 года нашей эры), что египтяне восторгались треугольником 3-4-5[3]. Берлинский папирус[en] из Среднего царства (до 1700 года до нашей эры) утверждает, что «квадрат, имеющий площадь 100, имеет ту же площадь, что и два меньших квадрата. Сторона одного равна ½ + ¼ стороне другого»[4]. Историк математики Роджер Л. Кук заметил: «трудно представить кого-либо, заинтересованного в таких вещах и не знающих теорему Пифагора» [3]. Однако Кук заметил, что ни в одном египетском тексте до 300 года до нашей эры не упоминается использование теоремы для нахождения сторон треугольника и имеется более простой путь построения прямого угла. Кук заключает, что предположение Кантора остаётся сомнительным — он предположил, что древние египтяне, возможно, знали теорему Пифагора, но «нет свидетельств, что они использовали её для построения прямых углов»[3].

Древняя Индия[править | править код]

Подробное рассмотрение темы: Индийская архитектура и Васту-шастра
Гопурам индусского храма Вирупакши в Хампи имеет подобные фракталу структуру, в которой части напоминают целое.

Наука Васту-шастра, правила архитектуры и планирования городов древней Индии, использовала симметричное рисование, называемое мандала. Для определения размеров зданий и их компонентов использовались сложные вычисления. Планирование предполагало интеграцию архитектуры с природой, отдельных частей структуры и древних верований, использующих геометрические орнаменты (янтры), симметрию и размещение по направлениям[en][65][66]. Однако ранние строители могли натолкнуться на математические пропорции случайно. Математик Жорж Ифрах заметил, что простые «хитрости» с верёвкой и колом могли быть использованы для разметки геометрических объектов, таких как эллипсы и прямые углы[5][67].

План храма Минакши, Мадурай, с 7-го века. Четверо ворот (пронумерованных I—IV) являются высокими гопурами.

Математика фракталов использовалась для того, чтобы здания имели универсальную притягательность, поскольку они обеспечивали наблюдателю чувство масштаба с любого расстояния. Например, в высоких гопурамах индусских храмов, таких как Храм Вирупакши в Хампи, построенном в XVII веке, и храм Кандарья-Махадева в группе храмов Кхаджурахо[en], у которых части и целое имеют одинаковые характеристики с фрактальной размерностью в границах от 1,7 до 1,8. Группа меньших башен (шикхара) вокруг более высокой центральной башни, которая представляет святую гору Кайлас, обиталище божества Шива, изображаемого в виде бесконечного повторения вселенных индуистской космологии[2][7].

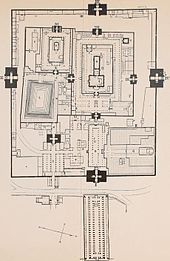
Храм Минакши в городе Мадурай является большим комплексом с множеством усыпальниц и улиц, расходящихся концентрично от храма согласно Шастрам. Четверо ворот являются высокими башнями (гопурамы) с повторяющейся структурой, подобной фракталу. Участки вокруг каждого святилища прямоугольны и окружены высокими каменными стенами[68].

Древняя Греция[править | править код]

Подробное рассмотрение темы: Архитектура Древней Греции, Золотое сечение, Пифагореизм и Евклидова геометрия
Парфенон был спланирован с использованием пифагорейских отношений.

Пифагор (569—475 года до нашей эры) и его последователи, пифагорейцы, считали, что «всё есть числа». Они наблюдали гармонию, получаемую звучанием с малыми целочисленными отношениями частот, и утверждали, что здания также должны планироваться с теми же отношениями. Греческое слово симметрия означало гармонию архитектурных форм с соблюдением точных отношений размеров от малых деталей до всего здания [5].

План Парфенона

Парфенон имеет длину 69,5 метров, ширину 30,9 метров и высоту 13,7 метров до карниза. Это даёт отношение ширины к длине 4:9, и то же самое отношение высоты к ширине. Собирая всё вместе, получим высота: ширина: длина = 16:36:81, 42:62:92. Прямоугольник 4:9 может быть построен как три последовательных прямоугольника с отношением сторон 3:4. Половина каждого прямоугольника тогда получается привычным прямоугольным треугольником 3:4:5, что позволяло проверить углы и стороны при помощи подходящей верёвки с узлами. Аналогично внутренняя область (наос) имеет пропорции 4:9 (21,44 метр ширины к 48,3 метров длины). Отношение диаметра внешних колонн (1,905 метров) к расстоянию между их центрами (4,293 метра) также равно 4:9[5].

Парфенон считается такими авторами, как Джон Юлиус Нарвич, «самым совершенным храмом дорийцев из когда-либо построенных»[69]. Тщательно разработанные архитектурные детали храма включают «тонкое соответствие между кривизной стилобата, плавное изменение толщины стен целлы и энтазис стобов»[69]. Энтазис — это едва уловимое уменьшение диаметра колонн. Стилобат — это платформа, на которой колонны стоят. Как и в других классических греческих храмах[70], платформа имеет небольшую параболическую кривизну (выпуклость), чтобы сливать дождевую вода и укрепить здание в случае землетрясения. Из-за этого колонны могли бы падать наружу, но, в действительности, наклонены слегка внутрь, так что если их продлить вверх, они встретятся в миле над зданием. Поскольку они все имеют одинаковую высоту, кривизна внешнего края стилобата отражается в архитрав и крышу над ним: «всё следует правилу построения по утончённым кривым»[71].

Золотое сечение известно с 300 года до нашей эры, когда Евклид описал метод геометрического построения[72]. Он утверждал, что золотое сечение использовалось как при планировании Парфенона и других древних греческих зданий, так и в скульптурах, картинах и вазах[73]. Более современные авторы, такие как Никос Салингарос, однако, сомневаются в этих утверждениях[74]. Эксперименты специалиста по информатике Джорджа Марковски не смогли найти какой-либо связи с золотым прямоугольником[62].

Исламская архитектура[править | править код]

Основная статья: Исламская архитектура
Львиный дворик комплекса Альгамбра имеет строгие пропорции, основанные на квадратных корнях из малых целых чисел.

Историк исламского искусства Антонио Фернандес-Пуэртас высказал предположение, что архитектурно-парковый ансамбль Альгамбра, подобно Кóрдовской соборной мечети в Кордове[75], был спроектирован с помощью испано-мусульманского фута (или кодо, около 0,62 метра). В дворцовом львином дворике пропорции составляют рад радикалов. Дворик представляет прямоугольник со сторонами 1 и √2 и имеет согласно теореме Пифагора диагональ √3. Серия продолжается числом √4 (дающим отношение 1:2), √5 и так далее. Декоративные узоры имеют аналогичные пропорции, √2 образует квадраты внутри окружностей и восьмиугольных звёзд, √3 образует шестиугольные звёзды. Нет свидетельств использования золотого сечения при проектировании Альгамбры[27][76]. Львиный дворик окружён Залом Двух Сестёр и Залом Абенсеррахов. Из центров этих двух залов и четырёх внутренних углов львиного дворика может быть нарисован правильный шестиугольник[77].

Мечеть Селимие, 1569—1575

Мечеть Селимие в городе Эдирне, Турция, была построена Мимаром Синаном таким образом, что михраб можно видеть с любой точки внутри здания. Очень большое внутреннее пространство оформлено в виде восьмиугольника, образованного 8 огромными столбами и покрытого круглым куполом диаметром 31,25 метр и высотой 43 метра. Восьмиугольник образован внутри квадрата с четырьмя полукуполами и четырьмя исключительно высокими (83 метра) минаретами. План здания выглядит как круг внутри восьмиугольника внутри квадрата[78].

Могольская архитектура[править | править код]

Основные статьи: Архитектура Великих Моголов, Фатехпур-Сикри и Источники и архитектура Тадж-Махал
Мавзолей Тадж-Махал с частью садов комплекса в городе Агра

Архитектура Великих Моголов, как видно в заброшенном имперском городе Фатехпур-Сикри и комплексе Тадж-Махал, имеет отличительное математическое устройство и сильную эстетику, опирающуюся на симметрию и гармонию[28][79].

Тадж-Махал служит примером монгольской архитектуры, одновременно представляющий рай[80] и показывающий своими размерами, симметрией и дорогим убранством могущество монгольского императора Шах-Джахана. Белый мраморный мавзолей, украшенный флорентийской мозаикой[en], главные ворота, ансамбль зданий, суды и дорожки образуют единый иерархический дизайн. Здания, включая мечеть, из красного песчаника на западе и почти идентичное здание, Джаваб, на востоке, служат поддержкой двусторонней симметрии комплекса. Чарбах[en] (сад в четырёх частях) имеет четыре части, символизирующие четыре реки рая, которые дают отражения мавзолея в воде. Каждая часть разделена на 16 партеров[81].

План комплекса Тадж-Махал. Главные ворота находятся справа, Мавзолей находится в центре, обрамлённый Мечетью (внизу) и джавабом. План содержит квадраты и восьмиугольники.

Комплекс Тадж-Махал был вычерчен на решётке, разделённой на более мелкие решётки. Ширина комплекса составляет 374 монгольских ярдов или зир[f]. Главная часть составляет три квадрата по 374 ярда. Они были разделены в местах базаров и караван-сараев на модули по 17 зир. Сад и террасы разделены на модули по 23 зиры шириной 368 зир (16 x 23). Мавзолей, мечеть и гостевой дом вычерчены на решётке 7 зир. Кох и Барро заметили, что если восьмиугольник, использованный неоднократно в комплексе, имеет стороны 7 единиц, тогда он имеет ширину 17 единиц[g], что может помочь объяснить выбор отношений в комплексе [82].

Христианская архитектура[править | править код]

Подробное рассмотрение темы: Архитектура церквей
Собор Святой Софии, Стамбул
a) План галереи (верхняя половина)
b) План первого этажа (нижняя половина)

Собор Святой Софии в городе Византий (ныне Стамбул), построенный в 537 году (и дважды перестроенный), был в течение тысячи лет[h] наибольшим кафедральным собором. Он стимулировал постройку многих более поздних зданий, включая Мечеть Султанахмет и другие мечети города. Архитектура Византии включает притвор, увенчанный круглым куполом и двумя полукуполами одного диаметра (31 метр), с пятью меньшими полукуполами, образующими апсиду и четыре круглых угла просторного прямоугольного внутреннего пространства[83]. Это интерпретировалось средневековыми архитекторами как представление земного внизу (квадратное основание) и святых небес сверху (устремлённый ввысь сферический купол)[84]. Император Юстиниан I использовал двух геометров, Исидора Милетского и Анфимия из Тралл, в качестве архитекторов. Исидор Милетский собирал труды Архимеда по стереометрии, которые оказали на него большое влияние[5][85].

Важность крещения в воде в христианстве была отражена в архитектуре баптистерий. Наиболее старый, Латеранский баптистерий в Риме, построенный в 440 году[86], установил тенденцию восьмиугольных баптистерий. Купель внутри этих строений была часто восьмиугольной, хотя наиболее крупный итальянский баптистерий в Пизе, построенный между 1152 и 1363 годами, имеет круглую форму с восьмиугольным резервуаром. Баптистерий имеет высоту 54,86 метра с диаметром 34,13 метра (отношение 8:5)[87]. Амвросий Медиоланский писал, что резервуары и баптистерии имели восьмиугольную форму, «поскольку на восьмой день[i] было вознесение»[88][89]. Аврелий Августин аналогично описывает восемь дней, как «вечность … освящённая воскрешением Христа»[89][90]. Восьмиугольный баптистерий Сан-Джованни, Флоренция, построенный между 1059 и 1128 годами, является одним из наиболее старых зданий в городе и одним из последних примеров традиций античности. Баптистерий крайне сильно повлиял на флорентийских архитекторов, и главные архитекторы той эпохи, включая Франческо Таленти, Альберти и Филиппо Брунеллески, использовали его в качестве модели классической архитектуры[91].

Число пять использовалось «восторженно»[92] в церкви Святого Иоанна Непомука (1721 год) в городе Зелена гора близ Ждяр-над-Сазавоу в Чешской республике, спроектированной Яном Блажей Сантини-Айхлем. Неф имеет форму круга, окружённого пятью парами колонн и пятью овальными куполами со стрельчатыми апсидами. Церковь имеет пять ворот, пять капелл, пять алтарей и пять звёзд. Легенда утверждает, что когда Ян Непомуцкий был предан мученической смерти, над его головой появилось пять звёзд[92][93]. Пятикратная архитектура может также символизировать пять ран Христа[en] и пять писем «Tacui» (латинский: «я храню молчание» [о секретах исповедальни])[94].

Антонио Гауди использовал широкий круг геометрических структур в храме Святого Семейства, Барселона, заложенного в 1882 году (и не завершённого к 2015 году). В них входят гиперболические параболоиды и гиперболоиды вращения,[14] замощения, арки с очертанием обратной цепной линии[en], катеноиды, геликоиды и линейчатые поверхности. Вариации геометрий комбинируются различными путями вокруг церкви. Например, на Фасаде Страстей Христовых храма Саграда-Фамилия Гауди собрал каменные «ветви» в форме гиперболических параболоидов, которые соприкасаются в вершинах без сходимости в одну точку. Для контраста в колоннаде имеются гиперболические параболоидные поверхности, гладко соединяющие другие структуры с образованием несвязных поверхностей. Гауди использовал природные узоры, являющиеся сами по себе математическими, с колоннами, напоминающими деревья, и притолоками, сделанными из базальта, естественным образом расколотого (при охлаждении расплавленной лавы) на шестиугольные колонны[en][12][13][14].

Собор Успения Святой Марии[en] в Сан-Франциско 1971 года имеет двускатную крышу, состоящую из восьми сегментов гиперболических параболоидов, расположенных так, что нижние горизонтальные сечения крыши являются квадратами, а верхние сечения — крестами. Квадратное здание имеет длину стороны 77,7 метров и высоту 57,9 метров[95]. Кафедральный собор Бразилии Оскара Нимейера (1970 год) использует гиперболоидную структуру другим образом. Собор построен из 16 идентичных бетонных лучей, каждый весом 90 тонн, расположенных в круге с образованием гиперболоида вращения. Белые лучи создают форму наподобие рук, молящихся небу[96][97][98][99].

Некоторые средневековые церкви в Скандинавии являются круглыми[en], включая четыре церкви на датском острове Борнхольм. Одна из самых старых, Эстерларская церковь[en] 1160 года, имеет круглый неф вокруг массивных каменных колонн, окружающих здание, пронизанный арками и украшенный фресками. Круговая структура имеет три этажа. Церковь, несомненно, была укреплена, а верхний этаж служил для защиты [100][101]

Математическое украшение[править | править код]

Исламское архитектурное украшение[править | править код]

Основная статья: Исламские геометрические орнаменты
Сложная геометрия и мозаики сотовых сводов в мечети шейха Лотфоллы, Исфахан, 1603—1619

Исламские здания часто украшаются геометрическими орнаментами[en], в которых, как правило, используются математические мозаики, образованные керамическими плитками (гирих, зулляйдж), которые могут быть простыми или украшены полосками[5]. В исламских орнаментах используются симметричные фигуры, такие как звёзды с шестью, восемью или кратными восьми углами. Некоторые из них основываются на мотивах печати Соломона, восьмиугольной звезды, сделанной из двух квадратов, повёрнутых на 45 градусов относительно друг друга[6]. Исламские орнаменты используют многие из 17 возможных групп обоев. В 1944 году Эдит Мюллер показала, что в украшении ансамбля Альгамбры используется 11 групп обоев, а в 1986 году Бранко Грюнбаум заявил, что нашёл 13 групп обоев в Альгамбре, настаивая при этом, что оставшиеся 4 группы не были найдены нигде в исламских орнаментах[6].

Современное архитектурное украшение[править | править код]

Подробное рассмотрение темы: Орнамент и Архитектура XXI века

К концу XX века новые математические конструкции, такие как фрактальная геометрия и апериодичные замощения, стали использоваться архитекторами для облицовки зданий [8]. В 1913 году архитектор-модернист Адольф Лоз в своей программной статье провозгласил: «Орнамент — это преступление»[9], оказав влияние на архитектурное мышление до конца XX века. В XXI веке архитекторы снова начали использовать орнаменты, но орнаменты XXI века сильно отличаются. Концертный зал и конференц-центр Хеннинга Ларсена[en] 2011 года в Рейкьявике выглядит подобно стене из кристаллов и сделан из больших блоков стекла[9]. Здание Равенсбурнского колледжа в Лондоне, построенное в 2010 году, покрыто 28 000 анодированных алюминиевых плиток красного, белого и коричневого цветов, связывая круглые окна различных размеров. Покрытие использует три типа плитки — равносторонний треугольник и два неправильных пятиугольника[10][11][j]. Библиотека в Канадзаве[en] (архитекторы Кадзуми Кудо и Хироси Хориба из Coelacanth K&H Architects) имеет декоративную решётку сделанную из маленьких круглых блоков стекла, вставленных в плоские бетонные стены [9].

Крепости[править | править код]

Европа[править | править код]

Подробное рассмотрение темы: Бастионная система укреплений

Архитектура фортификационных сооружений эволюционировала из средневековых укреплений[en], которые имели высокие каменные стены, к низкой симметричной бастионной системе укреплений, способной сопротивляться артиллерийскому обстрелу, между серединой XV и серединой XIX веков. Геометрия звёздной формы диктовалась необходимостью не допустить мёртвых зон, в которых атакующая пехота могла бы укрыться от огня защищающейся стороны. Стороны выступающих точек образовывали угол для возможности покрытия огнём всю поверхность и позволяли перекрёстный огонь (с двух сторон) с каждой выступающей точки. Хорошо известны архитекторы, разрабатывавшие такую защиту, — Микеланджело, Бальдассаре Перуцци, Винченцо Скамоцци и Себастьен Ле Претр де Вобан[102][103].

Историк архитектуры Зигфрид Гидион говорил, что фортификационные сооружения в виде звёзд имели определяющее влияние на компоновку идеальных городов эпохи Возрождения: «Эпоха Возрождения была загипнотизирована одним типом городов, который в течение полутора веков — от Филарета до Скамоцци — был отпечатком всех утопических схем, это был город в виде звезды»[104].

Китай[править | править код]

Тулоу в уезде Юндин[en], провинция Фуцзянь

В архитектуре Китая датируются XVI веком тулоу провинции Фуцзян — это круглые структуры общественной защиты, обычно со сплошными стенами и одной деревянной дверью, покрытой железом. Стены также покрыты крышами, которые немного наклонены во внешнюю и внутреннюю стороны, образуя кольцо. Центр кольца является открытым мощёным внутренним двором, часто со стеной, окружающей укреплённые галереи высотой до пяти этажей [105].

Экологические цели[править | править код]

Яхчал в городе Йезд, Иран.

Архитекторы могут также выбирать форму здания из экологических соображений[92]. Например, небоскрёб Мэри-Экс архитектурного бюро Foster and Partners, Лондон, известный как «Корнишон» за его подобную огурцу форму, является телом вращения. Здание разработано с использованием системы автоматизированного проектирования. Геометрия здания была выбрана не только исходя из эстетических причин, но и чтобы минимизировать вихри воздуха у основания здания. Вопреки явно кривой поверхности все панели стекла, образующие поверхность, являются плоскими, за исключением линзы на вершине здания. Большинство панелей квадратные, поскольку это позволяет вырезать стёкла с меньшими отходами[1].

Традиционный яхчал (ледяная яма) в Персии функционирует подобно испарительному охладителю. Над поверхностью структура имеет вид купола, но имеет подземное место хранения для льда, а иногда и для пищи. Подземное пространство и толстая теплонепроницаемая конструкция изолирует пространство круглый год. Внутреннее пространство часто остужалось ветроуловителями. Лёд был доступен летом для приготовления холодного десерта фалуде[106].

См. также[править | править код]

Пояснения

  1. ↑ В главе 3 книги 4 трактата Десять книг об архитектуре он обсуждает модули прямо [31]
  2. ↑ Римский фут[en]* равен примерно 0,296м.
  3. ↑ В современных алгебраических обозначениях эти отношения записываются как 1:1, √2:1, 4:3, 3:2, 5:3, 2:1.
  4. ↑ Конструктивизм оказал влияние на школу Баухаус и Ле Корбюзье, например[49]
  5. ↑ Пейс Никос Салингарос предположил противное[15], но неясно, какая математика в точности может быть воплощена в кривых церкви Ле Корбюзье[16].
  6. ↑ 1 зира равна примерно 0,86м.
  7. ↑ Квадрат, нарисованный вокруг восьмиугольника путём продления сторон добавляет четыре прямоугольных треугольников с гипотенузой 7, а две другие стороны равны √(49/2) или 4,9497..., примерно 5. Сторона квадрата тогда равна 5+7+5, что равно 17.
  8. ↑ Вплоть до того, как Севильский кафедральный собор был завершён в 1520.
  9. ↑ Шестой день страстной седмицы был Великой пятницей. Последующие воскресенье (воскрешение) было, таким образом восьмым днём[88].
  10. ↑ Предполагалось апериодичное замощение, чтобы избежать ритма в решётке, но, на практике, мозаика Пенроуза была слишком сложной, так что была выбрана решётка размером 2,625м по горизонтали и 4,55м по вертикали [11].

Примечания[править | править код]

  1. ↑ 1 2 3 Freiberger, 2007.
  2. ↑ 1 2 3 Rian, Park, Ahn, Chang, 2007, с. 4093–4107.
  3. ↑ 1 2 3 4 5 6 7 8 Cooke, 2011, с. 237–238.
  4. ↑ 1 2 Gillings, 1982, с. 161.
  5. ↑ 1 2 3 4 5 6 7 8 O'Connor, Robertson, 2002.
  6. ↑ 1 2 3 Rønning, 2009.
  7. ↑ 1 2 Fractals in Indian Architecture.
  8. ↑ 1 2 3 Williams, Ostwald, 2015, с. 1—24, chapter 48.
  9. ↑ 1 2 3 4 Gibberd, Hill, 2013.
  10. ↑ 1 2 Ravensbourne College, 2010.
  11. ↑ 1 2 3 Bizley.
  12. ↑ 1 2 3 Geometry of Antoni Gaudi.
  13. ↑ 1 2 3 Usvat.
  14. ↑ 1 2 3 4 Burry, Burry, Dunlop, Maher, 2001.
  15. ↑ 1 2 3 4 Salingaros.
  16. ↑ 1 2 Greene.
  17. ↑ 1 2 Biosphere.
  18. ↑ Williams, Ostwald, 2015, с. chapter 1. 25-31, Глава: Can There Be Any Relations Between Mathematica and Architecure.
  19. ↑ Витрувий, 1936, с. 16—21 Книга 1. Глава 1.
  20. ↑ Williams, Ostwald, 2015, с. chapter 1. 1–24.
  21. ↑ Williams, Ostwald, 2015, с. 3, chapter 48.
  22. ↑ Overview.
  23. ↑ Leyton, 2001.
  24. ↑ Stakhov, Olsen, 2009.
  25. ↑ Smith, 1870, с. 620.
  26. ↑ 1 2 Vitruvius, 2009, с. 8–9.
  27. ↑ 1 2 Tennant, 2003.
  28. ↑ 1 2 Rai, 1993, с. 19–48.
  29. ↑ van den Hoeven, van der Veen, 2010.
  30. ↑ Cucker, 2013, с. 103–106.
  31. ↑ Vitruvius.
  32. ↑ Williams, Ostwald, 2015, с. 42, 48.
  33. ↑ Roth, 1992, с. 36.
  34. ↑ Claridge, 1998, с. 204–5.
  35. ↑ Lancaster, 2005, с. 44–46.
  36. ↑ March, 1996, с. 54–65.
  37. ↑ Mathalino.com.
  38. ↑ Typ 525.69.781, Houghton Library, Harvard University
  39. ↑ Andersen, 2008, с. 117–121.
  40. ↑ Ruhl, 2011.
  41. ↑ Copplestone, 1963, с. 251.
  42. ↑ Wassell.
  43. ↑ Palladio, 1997, с. book I, chapter xxi, page 57.
  44. ↑ Scamozzi, 2003.
  45. ↑ Borys, 2014, с. 140–148 and passim.
  46. ↑ Beckh, 2015, с. 75 and passim.
  47. ↑ Выставка в Нижнем Новгороде, 1897, с. 292–294.
  48. ↑ Graefe, 1990, с. 110–114.
  49. ↑ 1 2 Hatherley, 2011.
  50. ↑ Rietveld Schröderhuis.
  51. ↑ Historic England[en] Arnos Grove Underground Station Архивная копия от 23 апреля 2018 на Wayback Machine Список национального достояния Англии[en]
  52. ↑ Moholy-Nagy, 1938, с. 46.
  53. ↑ Gamwell, 2015, с. 306.
  54. ↑ Le Corbusier, 2004.
  55. ↑ World Architecture Survey, 2010.
  56. ↑ Denver International Airport, 2013.
  57. ↑ Hahn, 2013.
  58. ↑ Salingaros, 2006, с. 139–141.
  59. ↑ Salingaros, 2006, с. 124–125.
  60. ↑ Gehry, Mudford, Koshalek, 2009.
  61. ↑ Garcetti, 2004.
  62. ↑ 1 2 Markowsky, 1992.
  63. ↑ Taseos, 1990.
  64. ↑ Gazale, 1999.
  65. ↑ Kramrisch, 1976.
  66. ↑ Sachdev, Tillotson, 2004, с. 155–160.
  67. ↑ Ifrah, 1998.
  68. ↑ King, 2005, с. 72.
  69. ↑ 1 2 Norwich, 2001, с. 63.
  70. ↑ Penrose, 1973, с. ch. II.3, plate 9.
  71. ↑ Stevens, 1962, с. 337–338.
  72. ↑ Начала Евклида. Book 6, Proposition 30.
  73. ↑ Archibald.
  74. ↑ Applications of the Golden Mean to Architecture Архивная копия от 4 марта 2016 на Wayback Machine
  75. ↑ Gedal, 2011.
  76. ↑ Irwin, 2011, с. 109–112.
  77. ↑ Robertson, 2007.
  78. ↑ Blair, Bloom, 1995.
  79. ↑ Michell, Pasricha, 2011.
  80. ↑ Parker, 2010, с. 224.
  81. ↑ Koch, 2006, с. 24 and passim.
  82. ↑ Koch, 2006, с. 104–109.
  83. ↑ Fazio, Moffett, Wodehouse, 2009.
  84. ↑ Gamwell, 2015, с. 48.
  85. ↑ Kleiner, Mamiya, 2008, с. 329.
  86. ↑ Menander, Brandt, Appetechia, Thorén, 2010.
  87. ↑ The Baptistery.
  88. ↑ 1 2 Huyser-Konig.
  89. ↑ 1 2 Kuehn, 1992, с. 53–60.
  90. ↑ Augustine of Hippo, 426, с. Book 22, Chapter 30.
  91. ↑ Kleiner, 2012, с. 355–356.
  92. ↑ 1 2 3 Simitch, Warke, 2014, с. 191.
  93. ↑ Zelená hora.
  94. ↑ Saint John of Nepomuk.
  95. ↑ Nervi.
  96. ↑ Brasilia Cathedral.
  97. ↑ Behrends, Crato, Rodrigues, 2012, с. 143.
  98. ↑ Emmer, 2012, с. 111.
  99. ↑ Mkrtchyan, 2013.
  100. ↑ Nordens kirker.
  101. ↑ Natur Bornholm.
  102. ↑ Duffy, 1975.
  103. ↑ Chandler, 1990.
  104. ↑ Giedion, 1962, с. 43.
  105. ↑ O'Neill, 2015.
  106. ↑ Mahdavinejad, Javanrudi, 2012.

Литература[править | править код]

на русском языке
  • Витрувий. Десять книг об архитектуре. — М.: Изд-во Всес. Академии архитектуры. (Серия «Классики теории архитектуры»), 1936. — 331 с.
  • Волошинов А. В. Математика и искусство: Книга для тех, кто не только любит математику или искусство, но и желает задуматься о природе прекрасного и красоте науки. 2-е издание, доработанное и дополненное. — М.: Просвещение, 2000. — 399 с. — ISBN 5-09-008033-X.
на других языках

Frode Rønning,. Islamic Patterns And Symmetry Groups. — University of Exeter, 2009.

Ссылки[править | править код]

Источник — https://wiki4.ru/w/index.php?title=Математика_и_архитектура&oldid=135599957