Задачи упаковки

Эта статья — о геометрических задачах упаковки. О числовых задачах упаковки см. Задача о ранце.

Задачи упаковки — это класс задач оптимизации в математике, в которых пытаются упаковать объекты в контейнеры. Цель упаковки — либо упаковать отдельный контейнер как можно плотнее, либо упаковать все объекты, использовав как можно меньше контейнеров. Многие из таких задач могут относиться к упаковке предметов в реальной жизни, вопросам складирования и транспортировки. Каждая задача упаковки имеет двойственную задачу о покрытии, в которой спрашивается, как много требуется некоторых предметов, чтобы полностью покрыть все области контейнера, при этом предметы могут накладываться.

В задаче упаковки задано:

• «контейнеры» (обычно одна двумерная или трёхмерная выпуклая область или бесконечная область)
• множество «объектов», некоторые из которых или все должны быть упакованы в один или несколько контейнеров. Множество может содержать различные объекты с заданными размерами, или один объект фиксированных размеров, который может быть использован несколько раз.

Обычно в упаковке объекты не должны пересекаться и объекты не должны пересекать стены контейнера. В некоторых вариантах цель заключается в нахождении конфигурации, которая упаковывает один контейнер с максимальной плотностью. В более общем виде целью является упаковка всех объектов в как можно меньше контейнеров. В некоторых вариантах наложение (объектов друг на друга и/или на границы контейнера) разрешается, но это наложение должно быть минимизировано.

Упаковка бесконечного пространства

Многие из этих задач, если размер контейнера увеличивается во всех направлениях, становятся эквивалентны задачам упаковки объектов как можно плотнее в бесконечном евклидовом пространстве. Эта задача относится к некоторому числу научных дисциплин и получает существенное внимание. Гипотеза Кеплера постулировала оптимальное решение упаковки шаров за сотни лет до того, когда была доказана Томасом Хейлзом. Получили внимание другие формы, включая эллипсоиды , платоновы и архимедовы тела , в том числе тетраэдры и димеры различных сфер .

Шестиугольная упаковка кругов

Шестиугольная упаковка кругов на 2-мерной евклидовой плоскости.

Основная статья: Упаковка кругов

Эти задачи математически отличаются от идей в теореме об упаковке кругов. Связанная задача упаковки кругов имеет дело с упаковкой кругов, возможно различных размеров, на поверхности, например, на плоскости или сфере.

Аналоги круга в других размерностях не могут быть упакованы с абсолютной эффективностью в размерностях, больших единицы (в одномерном пространстве аналог окружности — просто две точки). Таким образом, всегда останется незанятое пространство при упаковке исключительно кругами. Наиболее эффективный путь упаковки кругов, шестиугольная упаковка, даёт примерно 91 % эффективности.

Упаковка сфер в высших размерностях

Основная статья: Плотная упаковка равных сфер

В трёхмерном пространстве гранецентрированная решётка даёт оптимальную упаковку сфер. Доказано, что 8-мерная решётка E8 и 24-мерная решётка Лича оптимальны в соответствующих пространствах.

Упаковка платоновых тел в трёхмерных пространствах

Кубы легко могут быть расположены в трёхмерном пространстве так, что они полностью заполнят пространство. Наиболее естественная упаковка — кубические соты. Никакой другой правильный многогранник не может заполнить полностью пространство, но некоторые результаты известны. Тетраэдр может дать упаковку по меньшей мере 85 %. Одна из лучших упаковок правильными додекаэдрами основывается на вышеупомянутой гранецентрированной кубической решётке.

Тетраэдры и октаэдры вместе могут заполнить всё пространство в конфигурации, известной как тетраэдрально-октаэдральная мозаика.

Тело	Оптимальная плотность решётчатой упаковки
икосаэдры	0.836357…
додекаэдры	$(5+{\sqrt {5}})/8=0.904508...$
октаэдры	18/19 = 0.947368…

Моделирование, совмещающее методы локального улучшения со случайно сгенерированными упаковками, наводит на мысль, что решётчатые упаковки для икосаэдра, додекаэдра и октаэдра являются оптимальными и в более широком классе всех упаковок.

Упаковка в 3-мерные контейнеры

Сферы в евклидов шар

Задача нахождения наименьшего шара, в который можно упаковать без перекрытия $k$ открытых единичных шаров, имеет простой и полный ответ в $n$-мерном евклидовом пространстве, если $\scriptstyle k\leq n+1$, а в бесконечномерном гильбертовом пространстве — без ограничений. Имеет смысл описать его здесь с целью показать общую проблему. В этом случае возможна конфигурация $k$ попарно касающихся единичных шаров. Разместим центры в вершинах $a_{1},..,a_{k}$ правильного $\scriptstyle (k-1)$ мерного симплекса с ребром 2. Это легко сделать, начав с ортонормированного базиса. Лёгкие вычисления показывают, что расстояние от любой вершины до центра тяжести равно $\scriptstyle {\sqrt {2{\big (}1-{\frac {1}{k}}{\big )}}}$. Кроме того, любая другая точка пространства имеет большее расстояние по меньшей мере до одной из $\scriptstyle k$ вершин. В терминах включения шаров, $\scriptstyle k$ открытых единичных шаров, имеющих центры в точках $\scriptstyle a_{1},..,a_{k}$, попадают в шар радиуса $\scriptstyle r_{k}:=1+{\sqrt {2{\big (}1-{\frac {1}{k}}{\big )}}}$, который минимален для такой конфигурации.

Чтобы показать, что такая конфигурация оптимальна, допустим, что $\scriptstyle x_{1},...,x_{k}$ — центры $\scriptstyle k$ непересекающихся открытых единичных шаров, находящихся в шаре с радиусом $\scriptstyle r$ и центром в точке $\scriptstyle x_{0}$. Рассмотрим отображение из конечного множества $\scriptstyle \{x_{1},..x_{k}\}$ в $\scriptstyle \{a_{1},..a_{k}\}$, сопоставляющее $\scriptstyle x_{j}$ в $\scriptstyle a_{j}$ для всех $\scriptstyle 1\leq j\leq k$. Поскольку для всех $\scriptstyle 1\leq i<j\leq k$, $\scriptstyle \|a_{i}-a_{j}\|=2\leq \|x_{i}-x_{j}\|$, это отображение 1-липшицево и по теореме Киршбрауна оно распространяется до глобально определённого 1-липшицева отображения. В частности, существует точка $\scriptstyle a_{0}$, такая что для всех $\scriptstyle 1\leq j\leq k$ имеем $\scriptstyle \|a_{0}-a_{j}\|\leq \|x_{0}-x_{j}\|$, а следовательно, $\scriptstyle r_{k}\leq 1+\|a_{0}-a_{j}\|\leq 1+\|x_{0}-x_{j}\|\leq r$. Это показывает, что существуют $\scriptstyle k$ непересекающихся единичных открытых шаров в шаре радиусом $\scriptstyle r$ тогда и только тогда, когда $\scriptstyle r\geq r_{k}$. Заметим, что в случае бесконечномерного гильбертова пространства отсюда следует существование бесконечного числа непересекающихся единичных открытых шаров внутри шара радиуса $\scriptstyle r$ тогда и только тогда, когда $\scriptstyle r\geq 1+{\sqrt {2}}$. Например, единичные шары с центрами в $\scriptstyle {\sqrt {2}}e_{j}$, где $\scriptstyle \{e_{j}\}_{j}$ — ортонормальный базис, не пересекаются и содержатся в шаре радиуса $\scriptstyle 1+{\sqrt {2}}$ с центром в начале координат. Более того, для $\scriptstyle r<1+{\sqrt {2}}$ максимальное число непересекающихся открытых единичных шаров внутри шара радиуса r равно $\scriptstyle {\big \lfloor }{\frac {2}{2-(r-1)^{2}}}{\big \rfloor }$.

Сферы в параллелепипед

Задача определяет число сферических объектов заданного диаметра d, которые могут быть упакованы в прямоугольный параллелепипед размера a × b × c.

Одинаковые сферы в цилиндр

Задача определяет минимальную высоту h цилиндра с заданным радиусом R, в который упаковано n одинаковых шаров радиуса r (< R) .

Упаковка в 2-мерные контейнеры

Упаковка кругов

Основная статья: Упаковка кругов

Круги в круге

Оптимальная упаковка 10 кругов в круге

Основная статья: Упаковка кругов в круге

Упаковка n единичных кругов в как можно меньшую окружность. Задача тесно связана с распределением точек в единичной окружности с целью достичь наибольшего минимального расстояния d_n между точками.

Оптимальные решения были доказаны для n≤13 и для n=19.

Круги в квадрате

Оптимальная упаковка 15 кругов в квадрате

Основная статья: Упаковка кругов в квадрате

Упаковка n единичных кругов в как можно меньший квадрат. Задача тесно связана с распределением точек в единичном квадрате с целью достичь наибольшего минимального расстояния d_n между точками. Для преобразования двух этих формулировок задачи размер квадрата единичных кругов будет L=2+2/d_n.

Оптимальные решения были доказаны для n≤30.

Круги в равнобедренном прямоугольном треугольнике

Оптимальная упаковка 6 кругов в равнобедренном прямоугольном треугольнике

Основная статья: Упаковка кругов в равнобедренном прямоугольном треугольнике

Упаковка n единичных кругов в как можно меньший равнобедренный прямоугольный треугольник. Хорошие приближения известны для n<300 .

Круги в правильном треугольнике

Оптимальная упаковка 5 кругов в правильном треугольнике

Основная статья: Упаковка кругов в правильном треугольнике

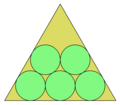
Упаковка n единичных кругов в как можно меньший правильный треугольник. Оптимальные решения известны для n<13, а для n<28 высказаны гипотезы.

Упаковка квадратов

Квадраты в квадрате

Оптимальная упаковка 10 квадратов в квадрате

Основная статья: Упаковка квадратов в квадрате

Упаковка n единичных квадратов в как можно меньший квадрат.

Оптимальные решения доказаны для n=1-10, 14-16, 23-25, 34-36, 62-64, 79-81, 98-100 и любого полного квадрата .

Незаполненное пространство асимптотически равно O(a^7/11) .

Квадраты в круге

Упаковка n квадратов в как можно меньший круг.

Минимальные решения:

Число квадратов	Радиус окружности
1	0.707…
2	1.118…
3	1.288…
4	1.414…
5	1.581…
6	1.688…
7	1.802…
8	1.978…
9	2.077…
10	2.121…
11	2.214…
12	2.236…

Упаковка прямоугольников

Одинаковые прямоугольники в прямоугольнике

Задача упаковки множественных копий одного прямоугольника размера (l,w) с разрешением поворота на 90° в больший прямоугольник размера (L,W) имеет несколько приложений, таких как загрузка коробок на поддоны и укладка древесно-стружечных плит.

Например, можно упаковать 147 прямоугольников размера 137x95 в прямоугольник размера 1600x1230 .

Различные прямоугольники в прямоугольнике

Задача упаковки прямоугольников с различной шириной и высотой в прямоугольник минимальной площади (но без ограничения на ширину и высоту такого прямоугольника) имеет важное приложение для сборки изображений в одно большое изображение. WEB-страница, загружающая одно большое изображение, часто обрабатывается быстрее в браузерах, чем при загрузке множества мелких изображений, поскольку требуется запрос каждого изображения с сервера.

Пример быстрого алгоритма, упаковывающего прямоугольники различной высоты и ширины в прямоугольник минимальной площади, — здесь.

Связанные задачи

В задачах замощения не должно быть ни промежутков, ни наложений. Много головоломок такого типа используют упаковку прямоугольников или полимино в прямоугольник большего размера или другую фигуру, близкую к квадрату.

Существует важная теорема о замощении прямоугольников (и прямоугольных параллелепипедов) в прямоугольники (прямоугольные параллелепипеды) без промежутков и наложений:

Прямоугольник a × b может быть упакован в ленту 1 × n тогда и только тогда, когда n делится на a или n делится на b

Теорема де Брёйна: прямоугольный параллелепипед может быть упакован гармоническим кирпичом a × a b × a b c, если параллелепипед имеет размеры a p × a b q × a b c r для некоторых натуральных чисел p, q, r (то есть параллелепипед кратен кирпичу.)

Изучение замощений плитками полимино в значительной степени касается двух классов задач — замощение прямоугольника конгруэнтными плитками и замощение набором плиток n-полимино прямоугольника.

Классическая головоломка второго вида — расположить все двенадцать плиток пентамино в прямоугольниках размером 3×20, 4×15, 5×12 или 6×10.

Упаковка неправильных объектов

Упаковка неправильных объектов является задачей, решение которой вряд ли возможно в замкнутой (аналитической) форме. Однако в науке об окружающем мире задача весьма важна. Например, неправильные частички почвы упаковываются различным образом при изменении размеров и формы частичек, что ведёт к существенным последствиям для растений по формированию корней и возможности перемещения воды в почве.

См. также

• Упаковка множеств
• Задача об упаковке в контейнеры
• Головоломка Слотобера — Граатсмы
• Головоломка Конвея
• Тетрис
• Задачи покрытия
• Задача о ранце
• Тетраэдральная упаковка
• Задача раскроя
• Контактное число
• Плотная упаковка равных сфер
• Случайная плотная упаковка

Литература

• S. Torquato, Y. Jiao. Dense packings of the Platonic and Archimedean solids // Nature. — 2009. — Т. 460, вып. 7257. — С. 876–879. — ISSN 0028-0836. — doi:10.1038/nature08239. — . — arXiv:0908.4107. — PMID 19675649.
• Hallard T. Croft, Kenneth J. Falconer, Richard K. Guy. Unsolved Problems in Geometry. — New York: Springer-Verlag, 1991. — С. 108–110. — ISBN 0-387-97506-3.
• J. Melissen. Packing 16, 17 or 18 circles in an equilateral triangle // Discrete Mathematics. — 1995. — Т. 145. — С. 333–342. — doi:10.1016/0012-365X(95)90139-C.
• Y. G. Stoyan, G. N. Yaskov. Packing identical spheres into a cylinder // International Transactions in Operational Research. — 2010. — Т. 17. — С. 51–70. — doi:10.1111/j.1475-3995.2009.00733.x.
• Eckard Specht. The best known packings of equal circles in a square  (неопр.) (20 мая 2010). Дата обращения: 25 мая 2010.
• P. Erdős, R. L. Graham. On packing squares with equal squares // Journal of Combinatorial Theory, Series A. — 1975. — Т. 19. — С. 119–123. — doi:10.1016/0097-3165(75)90099-0.
• A. Lodi, S. Martello, M. Monaci. Two-dimensional packing problems: A survey // European Journal of Operational Research. — Elsevier, 2002. — Т. 141. — С. 241–252. — doi:10.1016/s0377-2217(02)00123-6.
• A. Donev, F. Stillinger, P. Chaikin, S. Torquato. Unusually Dense Crystal Packings of Ellipsoids // Physical Review Letters. — 2004. — Т. 92, вып. 25. — doi:10.1103/PhysRevLett.92.255506. — . — arXiv:cond-mat/0403286.
• A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray, S. C. Glotzer. Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra // Nature. — 2009. — Т. 462, вып. 7274. — С. 773–777. — doi:10.1038/nature08641. — . — arXiv:1012.5138. — PMID 20010683.
• E. R. Chen, M. Engel, S. C. Glotzer. Dense Crystalline Dimer Packings of Regular Tetrahedra // Discrete & Computational Geometry. — 2010. — Т. 44, вып. 2. — С. 253–280. — doi:10.1007/s00454-010-9273-0.
• T. S. Hudson, P. Harrowell. Structural searches using isopointal sets as generators: Densest packings for binary hard sphere mixtures // Journal of Physics: Condensed Matter. — 2011. — Т. 23, вып. 19. — С. 194103. — doi:10.1088/0953-8984/23/19/194103.
• E. G. Birgin, R. D. Lobato, R. Morabito. An effective recursive partitioning approach for the packing of identical rectangles in a rectangle // Journal of the Operational Research Society. — 2010. — Т. 61. — С. 306–320. — doi:10.1057/jors.2008.141.
• Ross Honsberger. Mathematical Gems II. — The Mathematical Association of America, 1976. — ISBN 0-88385-302-7.
• D.A. Klarner, M.L.J Hautus. Uniformly coloured stained glass windows // Proceedings of the London Mathematical Society. — 1971. — Т. 23. — doi:10.1112/plms/s3-23.4.613.
• Eckard Specht. The best known packings of equal circles in an isosceles right triangle  (неопр.) (11 марта 2011). Дата обращения: 1 мая 2011.
• U. Betke, M. Henk. Densest lattice packings of 3-polytopes // Comput. Geom.. — 2000. — Т. 16. — С. 157–186.
• H. Minkowski. Dichteste gitterförmige Lagerung kongruenter Körper // Nachr. Akad. Wiss. Göttingen Math. Phys. KI. II. — 1904. — С. 311–355.
• Erich Friedman. Packing unit squares in squares: a survey and new results // The Electronic Journal of Combinatorics. — 2005. — Т. DS7. Архивировано 27 июля 2009 года.

Ссылки

• Weisstein, Eric W. Klarner's Theorem (англ.) на сайте Wolfram MathWorld.
• Weisstein, Eric W. de Bruijn's Theorem (англ.) на сайте Wolfram MathWorld.
• API для упаковки 3D-контейнера
• Упаковка 3D-коробок и цилиндров с вложением
• Упаковка двумерных прямоугольников в ортогональной таблице

Многие книги с головоломками, так же, как и математические журналы, содержат статьи об упаковках.

• Ссылки на различные статьи MathWorld по упаковкам
• Заметки MathWorld об упаковке квадратов.
• Erich’s Packing Center Архивная копия от 14 марта 2010 на Wayback Machine
• www.packomania.com Сайт с таблицами, графами, вычислениями, ссылками и т. д.
• «Box Packing» by Ed Pegg, Jr., the Wolfram Demonstrations Project, 2007.
• Наиболее известные упаковки одинаковых кругов в окружности, около 1100
• Circle packing challenge problem in Python